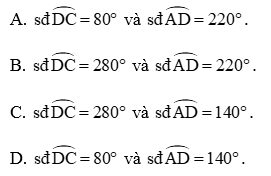Giải Toán 9 trang 112 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 112 Tập 1 trong Bài tập cuối chương 5 Toán lớp 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 112.

Giải Toán 9 trang 112 Tập 1 Kết nối tri thức

Bài 5.32 trang 112 Toán 9 Tập 1: Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng $OA=\sqrt{15}\text{\hspace{0.17em}\hspace{0.17em}cm}$  và OB = 4 cm. Khi đó:

A. Điểm A nằm trong (O), điểm B nằm ngoài (O).

B. Điểm A nằm ngoài (O), điểm B nằm trên (O).

C. Điểm A nằm trên (O), điểm B nằm trong (O).

D. Điểm A nằm trong (O), điểm B nằm trên (O).

Lời giải:

Đáp án đúng là: D

Vì $OA=\sqrt{15}\text{\hspace{0.17em}\hspace{0.17em}cm}<4\text{\hspace{0.17em}\hspace{0.17em}cm}$ nên điểm A nằm trong (O; 4 cm).

Vì OB = 4 cm nên điểm B nằm trên (O; 4 cm).

Vậy điểm A nằm trong (O), điểm B nằm trên (O).

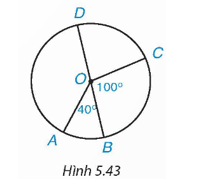
Bài 5.33 trang 112 Toán 9 Tập 1: Cho hình 5.43, trong đó BD là đường kính, $\widehat{AOB}=40°;\widehat{BOC}=100°.$

Khi đó:

Lời giải:

Đáp án đúng là: D

• Vì $\widehat{DOC}$  và $\widehat{BOC}$  là hai góc kề bù nên $\widehat{DOC}+\widehat{BOC}=180°$ .

Suy ra $\widehat{DOC}=180°-\widehat{BOC}=180°-100°=80°.$

Do đó $sđ\stackrel{⏜}{DC}=80°$ .

• Vì $\widehat{AOD}$  và $\widehat{AOB}$  là hai góc kề bù nên $\widehat{AOD}+\widehat{AOB}=180°$ .

Suy ra $\widehat{AOD}=180°-\widehat{AOB}=180°-40°=140°.$

Do đó $sđ\stackrel{⏜}{AD}=140°$ .

Vậy $sđ\stackrel{⏜}{DC}=80°$  và $sđ\stackrel{⏜}{AD}=140°$ .

Bài 5.34 trang 112 Toán 9 Tập 1: Cho hai đường tròn (A; R₁), (B; R₂), trong đó R₂ < R₁. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).

Khi đó:

A. AB < R₁ − R₂.

B. R₁ − R₂ < AB < R₁ + R₂.

C. AB > R₁ + R₂.

D. AB = R₁ + R₂.

Lời giải:

Đáp án đúng là: B

Áp dụng bất đẳng thức trong tam giác ABC, ta có:

AC – BC < AB < AC + BC.

Do đó R₁ − R₂ < AB < R₁ + R₂.

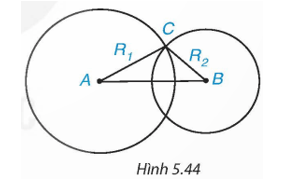
Bài 5.35 trang 112 Toán 9 Tập 1: Cho đường tròn (O; R) và hai đường thẳng a₁ và a₂. Gọi d₁, d₂ lần lượt là khoảng cách từ điểm O đến a₁ và a₂. Biết rằng (O) cắt a₁ và tiếp xúc với a₂ (H.5.45).

Khi đó:

A. d₁ < R, d₂ = R.

B. d₁ = R, d₂ < R.

C. d₁ > R, d₂ = R.

D. d₁ < R, d₂ < R.

Lời giải:

Đáp án đúng là: A

• Vì (O) cắt a₁ nên d₁ < R.

• Vì (O) tiếp xúc a₂ nên d₂ = R.

Vậy d₁ < R, d₂ = R.

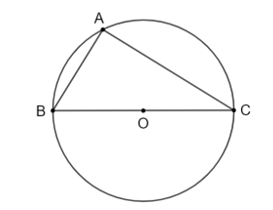
Bài 5.36 trang 112 Toán 9 Tập 1: Cho đường tròn (O) đường kính BC và điểm A (khác B và C).

a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).

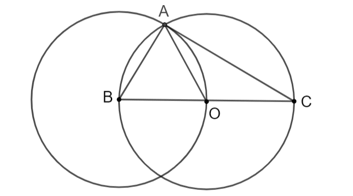
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.

c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.

Lời giải:

a)

Vì điểm A nằm trên đường tròn tâm O nên AO = BO = CO.

Tam giác ABC có AO là đường trung tuyến ứng với cạnh BC và $AO=\frac{1}{2}BC$  nên tam giác ABC vuông tại A.

Chiều ngược lại: Nếu tam giác ABC vuông tại A, gọi O là trung điểm của cạnh huyền BC thì ta có AO = BO = CO (tính chất đường trung tuyến trong tam giác vuông).

Từ đó ta có A, B, C thuộc đường tròn tâm O.

b)

Vì điểm A là giao điểm của hai đường tròn (O) và (B) nên A thuộc (O) đường kính BC nên tam giác BAC vuông tại A.

Tam giác ABO có AB = BO = AO nên tam giác ABO đều suy ra

$\widehat{ABO}=\widehat{AOB}=\widehat{BAO}=60°.$

Tam giác ABC vuông tại A nên $\widehat{B}+\widehat{C}=90°$ .

Suy ra $\widehat{C}=90°-\widehat{B}=90°-60°=30°.$

c) Ta có: $\widehat{AOB}+\widehat{AOC}=180°$  (hai góc kề bù)

Suy ra $\widehat{AOC}=180°-\widehat{AOB}=180°-60°=120°.$

Đường kính BC = 6 cm nên bán kính đường tròn (O) là: 6 : 2 = 3 (cm).

Độ dài cung AC là: $\frac{2\pi \cdot 3\cdot 120}{360}=2\pi \text{\hspace{0.17em}\hspace{0.17em}(cm)}$ .

Diện tích phần quạt chứa OA, OC là: $\frac{\pi R^2\cdot 120}{360}=\frac{3^2\pi \cdot 120}{360}=3\pi \left({\text{cm}}^2\right).$

Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay khác:

• Giải Toán 9 trang 113