Giải Toán 9 trang 46 Tập 1 Kết nối tri thức

---

Với Giải Toán 9 trang 46 Tập 1 trong Bài 7: Căn bậc hai và căn thức bậc hai Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 trang 46.

Giải Toán 9 trang 46 Tập 1 Kết nối tri thức

Luyện tập 3 trang 46 Toán 9 Tập 1:

a) Không sử dụng MTCT, tính: $\sqrt{6^2};\sqrt{{\left(-5\right)}^2};\sqrt{5}-\sqrt{{\left(\sqrt{5}-1\right)}^2}.$

b) So sánh 3 với $\sqrt{10}$ bằng hai cách:

– Sử dụng MTCT;

– Sử dụng tính chất của căn bậc hai số học đã học ở lớp 7: Nếu 0 ≤ a < b thì $\sqrt{a}<\sqrt{b}.$

Lời giải:

a) Ta có:

⦁ $\sqrt{6^2}=\left|6\right|=6.$

⦁ $\sqrt{{\left(-5\right)}^2}=\left|-5\right|=5.$

⦁ $\sqrt{5}-\sqrt{{\left(\sqrt{5}-1\right)}^2}=\sqrt{5}-\left|\sqrt{5}-1\right|=\sqrt{5}-\left(\sqrt{5}-1\right)=\sqrt{5}-\sqrt{5}+1=1.$

b) Cách 1. Sử dụng MTCT:

Bấm các phím $\boxed{\sqrt{}}\boxed{1}\boxed{0}\boxed{=}\boxed{S\iff D}$ màn hình hiện kết quả là 3,16227766.

Vì 3,16227766 > 3 nên $\sqrt{10}>3.$

Cách 2. Sử dụng tính chất của căn bậc hai số học đã học ở lớp 7: Nếu 0 ≤ a < b thì $\sqrt{a}<\sqrt{b}.$

Ta có $\sqrt{9}=\sqrt{3^2}=\left|3\right|=3.$

Vì 0 < 9 < 10 nên $\sqrt{9}<\sqrt{10}$ hay $3<\sqrt{10}.$

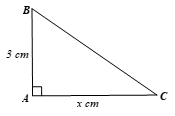
HĐ3 trang 46 Toán 9 Tập 1: Viết biểu thức tính độ dài cạnh huyền BC của tam giác vuông ABC, biết AC = 3 cm và AC = x cm.

Lời giải:

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 3² + x² = 9 + x².

Do đó $BC=\sqrt{9+x^2}$(cm) (vì BC > 0).

Vậy $BC=\sqrt{9+x^2}$(cm).

HĐ4 trang 46 Toán 9 Tập 1: Cho biểu thức $C=\sqrt{2x-1}.$

a) Tính giá trị của biểu thức tại x = 5.

b) Tại x = 0 có tính được giá trị của biểu thức không? Vì sao?

Lời giải:

a) Thay x = 5 vào biểu thức $C=\sqrt{2x-1},$ ta được:

$C=\sqrt{2\cdot 5-1}=\sqrt{9}=3.$

Vậy C = 3 khi x = 5.

b) Thay x = 0 vào biểu thức 2x – 1 dưới dấu căn của biểu thức C, ta được:

2.0 – 1 = –1 < 0, mà một số âm không có căn bậc hai số học nên ta không tính được giá trị của biểu thức C.

Vậy tại x = 0 ta không tính được giá trị của biểu thức C.

Luyện tập 4 trang 47 Toán 9 Tập 1: Cho căn thức $\sqrt{5-2x}.$

a) Tìm điều kiện xác định của căn thức.

b) Tính giá trị của căn thức tại x = 2.

Lời giải:

a) Điều kiện xác định của căn thức là 5 – 2x ≥ 0 hay –2x ≥ –5, suy ra $x\le \frac{5}{2}.$

b) Tại x = 2 (thỏa mãn điều kiện xác định), căn thức có giá trị là $\sqrt{5-2\cdot 2}=\sqrt{1}=1.$

Lời giải bài tập Toán 9 Bài 7: Căn bậc hai và căn thức bậc hai hay khác:

• Giải Toán 9 trang 45
• Giải Toán 9 trang 48