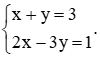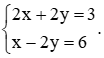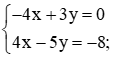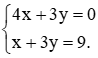Xét bài toán trong tình huống mở đầu. Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
Câu hỏi:
Xét bài toán trong tình huống mở đầu. Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
a) Lập hệ phương trình đối với hai ẩn x, y.
Trả lời:
Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
– Nếu tăng thêm 8 luống, nhưng mỗi luống trồng ít đi 3 cây cải bắp thì số cải bắp của cả vườn sẽ ít đi 108 cây;
Số luống trong vườn sau khi tăng thêm 8 luống là x + 8 (luống).
Khi mỗi luống trồng ít đi 3 cây cải bắp thì số cây bắp cải ở mỗi luống là: y – 3 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x + 8)(y – 3) = xy – 108
xy – 3x + 8y – 24 = xy – 108
3x – 8y = 84. (1)
– Nếu giảm đi 4 luống, nhưng mỗi luống trồng thêm 2 cây thì số cải bắp cả vườn sẽ tăng thêm 64 cây.
Số luống trong vườn sau khi giảm đi 4 luống là x – 4 (luống).
Khi mỗi luống trồng thêm 2 cây cải bắp thì số cây bắp cải ở mỗi luống là: y + 2 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x – 4)( y + 2) = xy + 64
xy + 2x – 4y – 8 = xy + 64
2x – 4y = 72
x – 2y = 36. (2)
Từ (1) và (2) ta có hệ phương trình 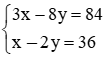 .
.
Từ phương trình thứ hai, ta có x = 2y + 36. Thế vào phương trình thứ nhất, ta được
3(2y + 36) – 8y = 84, tức là 6y + 216 – 8y = 84, suy ra 2y = 132 hay y = 66.
Từ đó x = 2y + 36 = 2 . 66 + 36 = 168.
Số cây cải bắp được trồng trên mảnh vườn đó là: 168 . 66 = 11 088 (cây).
Vậy số cây cải bắp được trồng trên mảnh vườn đó là 11 088 cây.