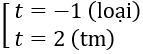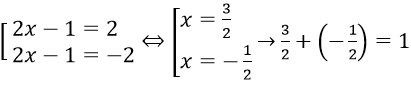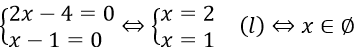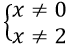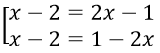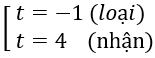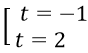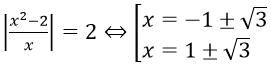Bài tập phương trình chứa dấu giá trị tuyệt đối chọn lọc, có lời giải - Toán lớp 10

---

Bài tập phương trình chứa dấu giá trị tuyệt đối chọn lọc, có lời giải

Với Bài tập phương trình chứa dấu giá trị tuyệt đối chọn lọc, có lời giải Toán lớp 10 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phương trình chứa dấu giá trị tuyệt đối từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Câu 1. Tập nghiệm S của phương trình |3x-2| = 3-2x là:

A. S = {-1; 1}        B. S = {-1}        C. S = {1}        D. S = {0}

Câu 2. Tập nghiệm S của phương trình |2x-1| = x-3 là:

A. S = {4/3}        B. S = ∅        C. S = {-2; 4/3}        D. S = {-2}

Câu 3. Tổng các nghiệm của phương trình |x² + 5x + 4| = x + 4 bằng:

A. -12        B. -6        C. 6        D. 12

Câu 4. Tổng các nghiệm của phương trình 4x(x-1) = |2x-1| + 1 bằng:

A. 0        B. 1        C. 2        D. -2

Câu 5. Phương trình: |2x-4| + |x-1| = 0 có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. Vô số

Câu 6. Gọi x₁, x₂ (x₁ < x₂) là hai nghiệm của phương trình |x² - 4x - 5| = 4x - 17. Tính giá trị biểu thức P = x₁² + x₂

A. P = 16        B. P = 58        C. P = 28        D. P = 22

Câu 7. Phương trình |2x + 1| = |x² - 3x - 4| có bao nhiêu nghiệm?

A. 0        B. 1        C. 2        D. 4

Câu 8. Phương trình: |x+2| + |3x-5| - |2x-7| = 0, có nghiệm là:

A. ∀x ∈ [-2; 5/3]        B. x = -3        C. x = 3        D. x = 4

Câu 9. Cho phương trình: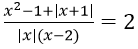. Có nghiệm là:

A. x = 1        B. x = 3        C. x = 4        D. x = 5

Câu 10. Phương trình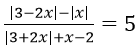. Có các nghiệm là:

A. x = -1/8, x = -7

B. x = -21/9, x = 2/23

C. x = -22/9, x = 1/23

D. x = -23/9, x = 3/23

Câu 11. Tập nghiệm của phương trình:|x-2| = |3x-5|  (1) là tập hợp nào sau đây ?

A. {3/2; 7/4}        B. {-3/2; 7/4}        C. {-7/4; -3/2}        D. {-7/4; 3/2}

Câu 12. Tập nghiệm của phương trình:|x-2| = 2x-1 là

A. S = {-1; 1}        B. S = {-1}        C. S = {1}        D. S = {0}

Câu 13. Phương trình: |3-x| + |2x+4| = 3, có nghiệm là

A. x = (-4)/3        B. x = -4        C. x = 2/3        D. Vô nghiệm

Câu 14. Số nghiệm của các phương trình (2x-1)² - 3|2x-1| - 4 = 0 là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 15. Số nghiệm của các phương trình 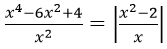là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Đáp án và hướng dẫn giải

   

Câu	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Đáp án	A	B	B	B	A	C	D	A	A	A	A	C	D	B	D

Câu 1. Chọn A

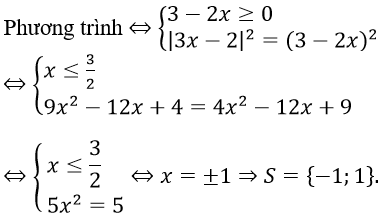
Câu 2. Chọn B

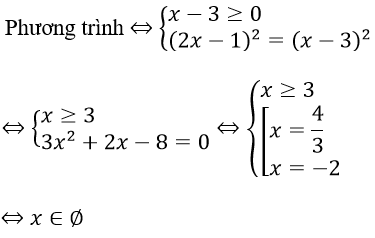
Vậy S = ∅

Câu 3. Chọn B

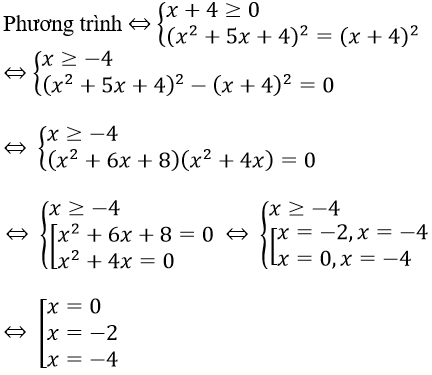
Có 0 + (-2) + (-4) = -6

Câu 4. Chọn B

Phương trình tương đương với 4x² - 4x - |2x-1| - 1 = 0

Đặt t = |2x-1|, t ≥ 0. Suy ra t² = 4x² - 4x + 1 ⇒ 4x² - 4x = t² - 1

Phương trình trở thành t² - 1 - t - 1 = 0 ⇔ t² - t - 2 = 0 ⇔

Với t = 2, ta có |2x-1| = 2

⇔

Câu 5. Chọn A

|2x - 4| + |x - 1| = 0 ⇔

Câu 6. Chọn C

Câu 7. Chọn D

Phương trình

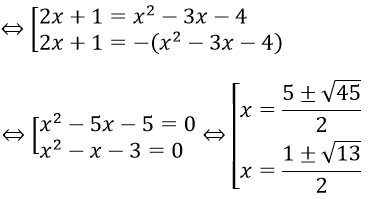
Câu 8. Chọn A

Trường hợp 1: x ≤ -2

Phương trình thành: -x - 2 - 3x + 5 + 2x - 7 = 0

⇔-2x = 4 ⇔ x = -2 (nhận)

Trường hợp 2: -2 ≤ x ≤ 5/3

Phương trình thành: x + 2 - 3x + 5 + 2x - 7 = 0 ⇔ 0x = 0 (luôn đúng)

Suy ra -2 ≤ x ≤ 5/3

Trường hợp 3: 5/3 ≤ x ≤ 7/2

Phương trình thành: x + 2 + 3x - 5 + 2x - 7 = 0 ⇔ 6x = 10 ⇔ x = 5/3 (nhận)

Trường hợp 4: x > 7/2

Phương trình thành: x + 2 + 3x -5 - 2x + 7 = 0 ⇔ 6x = -4

⇔ x = (-2)/3 (loại)

Vậy S = [-2; 5/3]

Câu 9. Chọn A

Điều kiện:

Phương trình thành x² - 1 + |x + 1| = 2|x|(x - 2)

TH1: x < -1

Phương trình thành x² - 1 - x - 1 = 2(-x)(x-2) ⇔ 3x² - 5x - 2 = 0

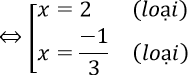
TH2: -1 ≤ x ≤ 0

Phương trình thành x² - 1 + x + 1 = -2x(x-2) ⇔ 3x² - 3x = 0

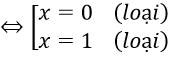
TH3: x > 0

Phương trình thành x² - 1 + x + 1 = 2x(x-2) ⇔ x² - 5x = 0

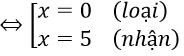
Câu 10. Chọn A

Điều kiện: |3 + 2x| + x - 2 ≠ 0

Phương trình thành |3 - 2x| - |x| = 5|3 + 2x| + 5x - 10

TH1: x < (-3)/2

Phương trình thành 3 - 2x + x = -15 - 10x + 5x - 10 ⇔ 4x = -28 ⇔ x = -7   (nhận)

TH2: (-3)/2 ≤ x ≤ 0

Phương trình thành 3 - 2x + x = 15 + 10x + 5x - 10 ⇔ 16x = -2 ⇔ x = -1/8   (nhận)

TH3: 0 < x < 3/2

Phương trình thành 3 - 2x - x = 15 + 10x + 5x - 10 ⇔ 18x = -2 ⇔ x = -1/9   (loại)

TH4: x ≥ 3/2

Phương trình thành -3 + 2x - x = 15 + 10x + 5x - 10 ⇔ 14x = -8

⇔ x = -4/7   (loại)

Câu 11. Chọn A

Ta có

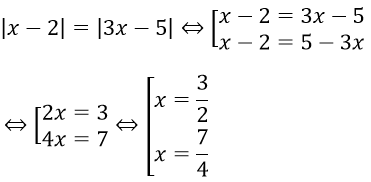
Câu 12. Chọn C

Ta có |x - 2| = 2x - 1 ⇔ 2x - 1 ≥ 0 và

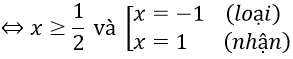
Vậy S = {1}

Câu 13. Chọn D

Trường hợp 1: x < -2

Phương trình thành 3 - x - 2x - 4 = 3 ⇔ 3x = -4 ⇔ x = (-4)/3   (loại)

Trường hợp 2: -2 ≤ x ≤ 3

Phương trình thành 3 - x + 2x + 4 = 3 ⇔ x = -4   (loại)

Trường hợp 3: x > 3

Phương trình thành x - 3 + 2x + 4 = 3 ⇔ 3x = 2 ⇔ x = 2/3   (loại)

Vậy S = ∅

Câu 14. Chọn B

Đặt t = |2x - 1|, t ≥ 0

Phương trình trở thành t² - 3t - 4 = 0 ⇔

Với t = 4 ta có |2x - 1| = 4 ⇔ 2x - 1 = ±4 ⇔ x = 5/2 hoặc x = -3/2

Vậy phương trình có nghiệm là x = -3/2 và x = 5/2

Câu 15. Chọn D

ĐKXĐ: x ≠ 0. Đặt t = |(x² - 2)/x|, t ≥ 0

Phương trình trở thành t² - t - 2 = 0 ⇔

Với t = 2 ta có

Vậy phương trình có nghiệm là x = -1 ± √3 và x = 1 ± √3