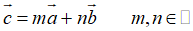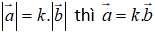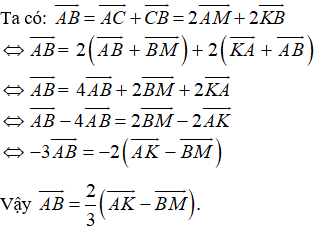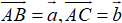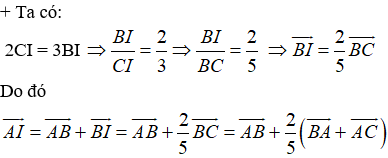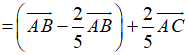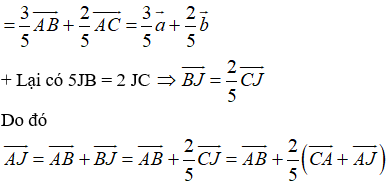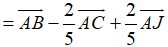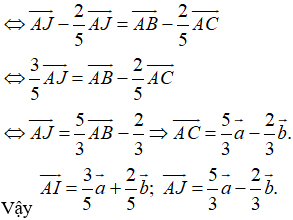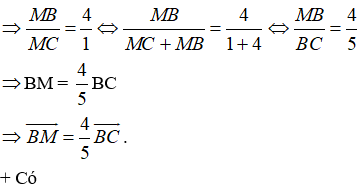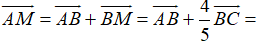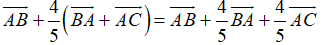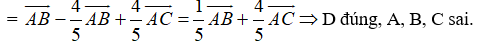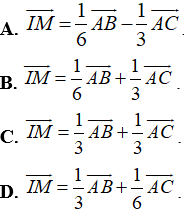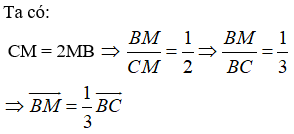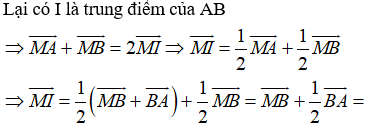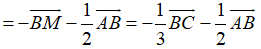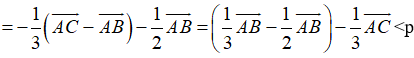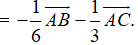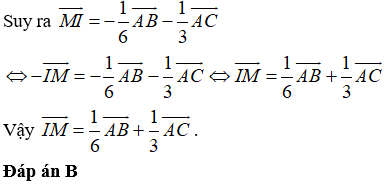Cách phân tích một vecto theo hai vecto không cùng phương cực hay, chi tiết - Toán lớp 10
Cách phân tích một vecto theo hai vecto không cùng phương cực hay, chi tiết
Với Cách phân tích một vecto theo hai vecto không cùng phương cực hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phân tích một vecto theo hai vecto không cùng phương từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
A. Phương pháp giải
Sử dụng định lý về phân tích vecto:
Phân tích vecto: Cho hai vecto không cùng phương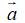 
, 
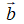
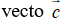
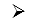
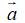
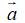
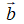
. Khi đó mọi 
đều được phân tích duy nhất: 
Sử dụng quy tắc hình bình hành, quy tắc 3 điểm,công thức trung điểm, trọng tâm…
Nếu hai vecto ; cùng hướng và 
Nếu hai vecto ; ngược hướng và 
B. Ví dụ minh họa
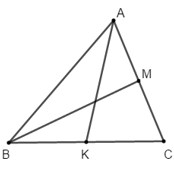
Ví dụ 1: Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích vecto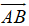 
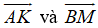
theo hai vecto 
.
Hướng dẫn giải:
Vì M là trung điểm của AC nên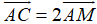 
Vì K là trung điểm của BC nên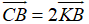 
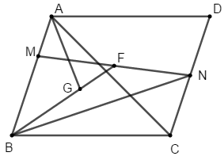
Ví dụ 2: Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM =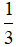 
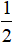
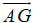
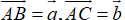
AB, CN = 
CD. Gọi G là trọng tâm của tam giác BMN. Hãy phân tích 
theo hai vecto 
.
Hướng dẫn giải:
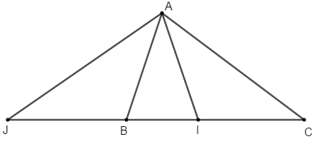
Ví dụ 3: Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI và J là điểm nằm trên tia đối của BC sao cho 5JB = 2JC. Phân tích vecto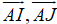 
theo 
Hướng dẫn giải:
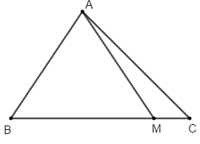
Ví dụ 4: Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 4MC. Khi đó:
Hướng dẫn giải:
Ta có:
MB = 4MC
Đáp án D
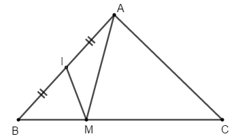
Ví dụ 5: Cho tam giác ABC có M thuộc cạnh BC sao cho CM = 2MB và I là trung điểm của AB. Đẳng thức nào sau đây đúng?
Hướng dẫn giải:
