Ứng dụng tam thức bậc hai, bất phương trình bậc hai vào các bài toán thực tế (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Ứng dụng tam thức bậc hai, bất phương trình bậc hai vào các bài toán thực tế lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Ứng dụng tam thức bậc hai, bất phương trình bậc hai vào các bài toán thực tế.

Ứng dụng tam thức bậc hai, bất phương trình bậc hai vào các bài toán thực tế (bài tập + lời giải)

1. Phương pháp giải

Để giải bài toán ứng dụng tam thức bậc hai, bất phương trình giải các bài toán thực tế, ta thực hiện các bước sau:

Bước 1. Đặt ẩn cho đại tượng cần tìm và các biểu diễn các đại lượng liên quan.

Bước 2. Dựa vào giả thiết, lập bất phương trình bậc hai tương ứng.

Bước 3. Giải bất phương trình bậc hai dựa vào định lí dấu của tam thức bậc hai.

Bước 4. Kết luận.

2. Ví dụ minh họa

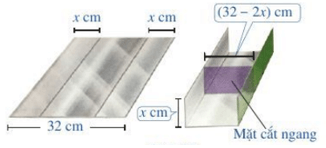
Ví dụ 1. Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình vẽ).

Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 120 cm². Rãnh nước phải có độ cao ít nhất là bao nhiêu xăng–ti–mét?

Hướng dẫn giải:

Gọi kích thước của mặt cắt ngang là x (cm) và 32 – 2x (cm).

Khi đó diện tích mặt cắt ngang là S(x) = x(32 – 2x) (cm²)

Diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 120 cm² khi và chỉ khi x(32 – 2x) ≥ 120

⇔ –2x² + 32x – 120 ≥ 0

⇔ x Î [6; 10]

Vậy rãnh nước phải có độ cao ít nhất 6 cm.

Ví dụ 2. Một công ty bình gia dụng sản xuất bình đựng nước thấy rằng khi đơn giá của bình đựng nước là x nghìn đồng thì doanh thu R (tính theo đơn vị nghìn đồng) sẽ là

R(x) = –560x² + 50 000x.

a) Theo mô hình doanh thu này thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán bình đựng nước bằng 0 (tức là không có người mua)?

b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng?

Hướng dẫn giải:

a) Doanh thu từ việc bán bình đựng nước bằng 0 tức là

R(x) = –500x² + 50 000x = 0 ⇔ x = 0 hoặc x = 89

Vậy theo mô hình đã cho, với đơn giá 89 nghìn đồng thì công ty không có doanh thu. (Đơn giá quá cao dẫn đến không có người mua hàng)

b) Doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng, tức là

–560x² + 50 000x > 1 000 000

⇔ 56x² – 5 000x + 100 000 < 0

⇔ 30,25 < x < 59,04

Vậy với đơn giá của bình đựng nước khoảng 31 nghìn đồng đến 59 nghìn đồng thì doanh thu vượt mức 1 tỉ đồng.

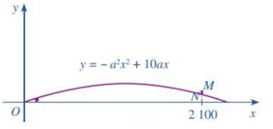
Ví dụ 3. Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng toạ độ Oxy, khẩu đại bác được biểu thị bằng điểm O (0; 0) và bia mục tiêu được biểu thị bằng đoạn thẳng MN với M (2 100; 25) và N (2 100; 15).

Xạ thủ cần xác định parabol y = –a²x² + 10ax (a > 0) mô tả quỹ đạo chuyển động của viên đạn sao cho viên đạn bắn ra từ khẩu đại bác phải chạm vào bia mục tiêu. Tìm giá trị lớn nhất của a để xạ thủ đạt được mục đích trên.

Hướng dẫn giải:

Tại vị trí x = 2 100, độ cao của viên đạn là:

y = –a².2 100² + 10a.2 100 = –4 410 000a² + 21 000a

Viên đạn chạm được vào bia mục tiêu khi và chỉ khi a thoả mãn các bất phương trình sau:

$2100\le \frac{10}{a}$ (5);

–4 410 000a² + 21 000a ≤ 25 (6);

–4 410 000a² + 21 000a ≥ 15 (7)

Giải (5): $2100\le \frac{10}{a}$⇔ $\frac{1}{a}\ge 210$ ⇔ $a\le \frac{1}{210}$

                Vì a > 0 nên a$\in \left(0;\frac{1}{210}\right]$.

Giải (6): –4 410 000a² + 21 000a ≤ 25

           ⇔ 4 410 000a² – 21 000a + 25 ≥ 0

           ⇔ (2 100a – 5)² ≥ 0.

Bất phương trình này đúng ∀a > 0.

Giải (7): –4 410 000a² + 21 000a ≥15

           ⇔ 4 410 000a² – 21 000a + 15 ≤ 0

           $\iff \frac{1}{420}–\frac{\sqrt{10}}{2100}\le a\le \frac{1}{420}+\frac{\sqrt{10}}{2100}$

           $\iff a\in \left[\frac{1}{420}–\frac{\sqrt{10}}{2100};\frac{1}{420}+\frac{\sqrt{10}}{2100}\right]$

Do $\frac{1}{420}–\frac{\sqrt{10}}{2100}>0$ và $\frac{1}{420}+\frac{\sqrt{10}}{2100}<\frac{1}{210}$

Nên $\left(0;\frac{1}{210}\right]\cap \left[\frac{1}{420}–\frac{\sqrt{10}}{2100};\frac{1}{420}+\frac{\sqrt{10}}{2100}\right]=\left[\frac{1}{420}–\frac{\sqrt{10}}{2100};\frac{1}{420}+\frac{\sqrt{10}}{2100}\right]$

Vì thế, viên đạn chạm được vào bia mục tiêu khi và chỉ khi $a\in \left[\frac{1}{420}–\frac{\sqrt{10}}{2100};\frac{1}{420}+\frac{\sqrt{10}}{2100}\right]$

Vậy giá trị lớn nhất của a là $\frac{1}{420}+\frac{\sqrt{10}}{2100}$.

3. Bài tập tự luyện 

Bài 1. Một công ty du lịch báo giá tiền cho chuyến tham quan của một nhóm khách du lịch như sau: 50 khách đầu tiên với giá 300 000đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ thêm một người, giá vé sẽ giảm 5 000 đồng/người cho toàn bộ hành khách. Biết rằng chi phí thực sự cho chuyến đi là 15 080 000 đồng. Số người của nhóm du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ?

A. 58;

B. 55;

C. 60;

D. 65.

Bài 2. Công ty An Bình báo giá tiền cho chuyến tham quan của một nhóm khách du lịch như sau: 10 khách đầu tiên với giá 800 000đồng/người. Nếu có nhiều hơn 10 người đăng kí thì cứ thêm một người, giá vé sẽ giảm 10 000 đồng/người cho toàn bộ hành khách. Biết rằng chi phí thực sự cho chuyến đi là 700 000 đồng/người. Số người của nhóm du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ?

A. 25;

B. 15;

C. 20;

D. 30.

Bài 3. Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất Q sản phẩm là Q² + 180Q + 140 000 (nghìn đồng). Giả sử giá mỗi sản phẩm bán ra thị trường là 1 200 nghìn đồng. Xí nghiệp cần sản xuất số sản phẩm là bao nhiêu để không bị lỗ?

A. Từ 157 đến 835;

B. Từ 164 đến 857;

C. Từ 164 đến 835;

D. Từ 157 đến 857.

Bài 4. Một viên đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu là 500 m/s, hợp với phương ngang một góc 45°. Biết rằng bỏ qua sức cản của không khí, quỹ đạo chuyển động của một vật ném xiên sẽ tuân theo phương trình

$y=–\frac{g}{2{v^2}_{0}co{s}^2\alpha }{x}^2+xtan\alpha .$

Trong đó x là khoảng cách (tính bằng mét) vật bay theo phương ngang, vận tốc ban đầu v_o của vật hợp với phương ngang một góc a và g = 9,8 m/s² là gia tốc trọng trường. Để viên đạn bay qua ngọn núi cao 4 000 mét thì khẩu pháo phải đặt cách chân núi một khoảng cách là

A. Từ 4 550 m đến 20 067 m;

B. Từ 4 550 m đến 20 543 m;

C. Từ 4 967 m đến 20 067 m;

D. Từ 4 967 m đến 20 543 m.

Bài 5. Xét hệ tọa độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây. Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất?

A. Từ 0 đến 4 giây;

B. Từ 0 đến 3,55 giây;

C. Từ 0 đến 2,55 giây;

D. Từ 0 đến 4,05 giây.

Hướng dẫn giải:

Đáp án đúng là: C

Phương trình của parabol là $h=h\left(t\right)=a{t}^2+bt+c$ (a ≠ 0), trong đó h là độ cao, t là thời gian, a, b, c là các hằng số cần tìm.

Quỹ đạo của quả bóng là một parabol đi qua điểm A(0; 0,2) nên thay t = 0 và h = 0,2 vào hàm số ta được: c = 0,2. 

Khi đó: h = h(t) = at² + bt + 0,2.

Lại có quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.

Do đó quỹ đạo của bóng là parabol đi qua các điểm có tọa độ (1; 8,5) và (2; 6)

Ta có hệ: $\left\{\begin{array}{l}8,5=a+b+0,2\\ 6=a.4+b.2+0,2\end{array}\right.$

$\iff \left\{\begin{array}{l}8,3=a+b\\ 5,8=4a+2b\end{array}\right.$

 $\iff \left\{\begin{array}{l}a=\frac{–27}{5}\\ b=\frac{137}{10}\end{array}\right.$

Vậy hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng là:

$h=h\left(t\right)=–\frac{27}{5}{t}^2+\frac{137}{10}t+0,2$

Bóng chưa chạm đất khi và chỉ khi h > 0

⇔ $–\frac{27}{5}{t}^2+\frac{137}{10}t+0,2>0$

⇔ –0,01 < t < 2,55

Vậy trong khoảng thời gian từ 0 đến 2,55 giây thì bóng vẫn chưa chạm đất. 

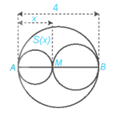
Bài 6. Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạnAB, đặt AM = x (hình vẽ). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Giá trị nào của x thì diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ?

A. 2;

B. 3,5;

C. 4;

D. 1,5.

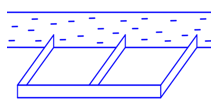
Bài 7. Một người nông dân có 6 triệu đồng để làm một hàng rào chữ E dọc theo một con sông (như hình vẽ) làm một khu đất có hai phần là hình chữ nhật để trồng rau. Đối với mặt hàng rào song song bờ sông thì chi phí nguyên vật liệu là 60 000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 40 000 đồng một mét.

Diện tích lớn nhất của khu đất rào thu được là

A. 1245;

B. 1 250;

C. 1 255;

D. 1 260.

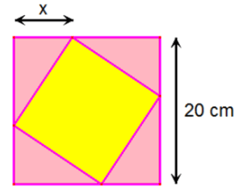
Bài 8. Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20 cm, tạo thành bốn tam giác xung quanh như hình vẽ.

Giá trị của x để diện tích viên gạch không vượt quá 208 cm² là

A. 8 ≤ x ≤ 12;

B. 6 ≤ x ≤ 14;

C. 12 ≤ x ≤ 14;

D. 12 ≤ x ≤ 18.

Bài 9. Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 30 000 đồng một chiếc và mỗi tháng cơ sở bán được trung bình 3 000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 30 000 đồng mà cứ tăng giá thêm 1 000 đồng thì mỗi tháng sẽ bán ít hơn 100 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 18 000. Hỏi cơ sở sản xuất phải bán với giá mới là bao nhiêu để đạt lợi nhuận lớn nhất?

A. 39 000;

B. 43 000;

C. 40 000;

D. 42 000.

Bài 10. Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có x con cá (x ∈ ℕ^*) thì trung bình mỗi con cá sau một vụ cân nặng là 480 – 20x (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau mỗi vụ thu hoạch được nhiều cá nhất?

A. 10;

B. 12;

C. 9;

D. 24.