Vị trí tương đối của 2 điểm với đường thẳng: cùng phía, khác phía - Toán lớp 10

---

Vị trí tương đối của 2 điểm với đường thẳng: cùng phía, khác phía

Với Vị trí tương đối của 2 điểm với đường thẳng: cùng phía, khác phía Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Vị trí tương đối của 2 điểm với đường thẳng: cùng phía, khác phía từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

Cho đường thẳng d: ax + by + c = 0 và hai điểm M( x_M; y_M); N(x_N; y_N) không nằm trên d. Khi đó:

+ Hai điểm M ; N nằm cùng phía đối với đường thẳng d khi và chỉ khi:

( ax_M + by_M + c) .( ax_N + by_N + c) > 0

+ Hai điểm M ; N nằm khác phía đối với đường thẳng d khi và chỉ khi:

( ax_M + by_M + c) .( ax_N + by_N + c) < 0

B. Ví dụ minh họa

Ví dụ 1: Cho đường thẳng d: x+ 2y- 10 =0 và hai điểm A( 1; -3) và B( 5;-4) . Chọn mệnh đề đúng :

A. Hai điểm A và B nằm cùng phía so với đường thẳng d.

B. Hai điểm A và B nằm khác phía so với đường thẳng d.

C. Có một điểm nằm trên đường thẳng d.

D. Khoảng cách hai điểm AB là 5.

Lời giải

Đặt f( x; y) = x + 2y - 10.

+ Ta có f(1; -3) = 1 + 2.(-3) - 10 = -15

Và f( 5; -4) = 5 + 2.(-4) - 10 = - 13

⇒ f( 1; -3) . f( 5; -4) > 0

⇒ Hai điểm A và B nằm cùng phía so với đường thẳng d.

+ Khoảng cách hai điểm A và B là: AB =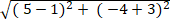

Chọn A.

Ví dụ 2: Cho đường thẳng d: 2x - y + 1 = 0 và ba điểm A(0; -3); B( -1; -1) và C(-3; 2) .

Tìm mệnh đề sai?

A. Hai điểm A và C nằm khác phía so với đường thẳng d.

B. Có ít nhất một điểm nằm trên đườngthẳng d.

C. Có không ít hơn hai điểm không thuộc đường thẳng d

D. Hai điểm A và B nằm cùng phía so với đường thẳng d.

Lời giải

Đặt f( x; y) = 2x - y + 1.

    f(0; -3) = 2.0 - (-3) + 1 = 4

    f(-1; -1) = 2.(-1) – (-1) + 1 = 0

    f(-3; 2) = 2.(-3) – 2 + 1 = - 7

Suy ra:

    Hai điểm A và C nằm khác phía so với đường thẳng d.

    Điểm B thuộc đường thẳng d; hai điểm A và C không thuộc đường thẳng d.

⇒ A; B và C đúng ; D sai.

Chọn D.

Ví dụ 3. Cho đường thẳng d: 3x + 4y – 5 = 0 và 2 điểm A( 1; 3) ; B( 2; m) . Tìm m để A và B nằm cùng phía đối với d?

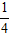
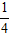
A. m < 0    B. m > -    C. m > 1    D. m = -

Hướng dẫn giải

Hai điểm A và B nằm về hai phía của đường thẳng d khi và chỉ khi:

( 3 + 12 - 5)(6 + 4m - 5) < 0 hay m > -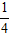

Chọn B.

Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: 3x + 4y - 5 = 0 và hai điểm A( 1; 3) và B ( 2; m). Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d?

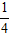
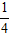
A. m < 0 .    B. m > -    C. m > - 1    D. m = -

Lời giải

Đặt f( x; y) = 3x + 4y - 5.

Để hai điểm A và B nằm cùng phía đối với d khi và chỉ khi:

f(A).f( B) > 0 ⇔ ( 3.1 + 4.3 - 5).( 3.2 + 4.m - 5) > 0

⇔ 10.( 1 + 4m) > 0 ⇔ 1 + 4m > 0 ⇔ m > -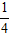

Chọn B.

Ví dụ 5. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: 4x - 7y + m = 0 và hai điểm A( 1; 2) và B(-3; 4). Tìm tất cả các giá trị của tham số m để d và đoạn thẳng AB có điểm chung.

A. 10 ≤ m ≤ 40    B. m > 40 hoặc m < 10    C. 10 < m < 40    D. m < 10

Lời giải

Đoạn thẳng AB và d: 4x - 7y + m = 0 có điểm chung khi và chỉ khi

Điểm A( hoặc điểm B) thuộc đường thẳng d hoặc hai điểm A và B nằm khác phía so với đường thẳng d.

+ Nếu A thuộc đường thẳng d thì: 4.1 - 7.2 + m = 0 ⇔ m = 10.

+ Nếu điểm B thuộc đường thẳng d thì: 4.(-3) – 7. 4 + m = 0 ⇔ m = 40.

+ Nếu hai điểm A và B nằm khác phía so với đường thẳng d khi đó đoạn thẳng AB sẽ cắt đường thẳng d.

⇒ ( 4x_A - 7y_A + m) .( 4x_B - 7y_B + m) < 0

⇔ ( m - 10) .( m - 40) < 0 ⇔ 10 < m < 40.

Kết hợp các trường hợp, vậy để đường thẳng d có điểm chung với đoạn thẳng AB thì
10 ≤ m ≤ 40.

Chọn A.

Ví dụ 6. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: và hai điểm A(1; 2) ; B(-2; m). Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d?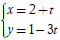

A. m > 13    B. m ≥ 13    C. m < 13    D. m = 13

Lời giải

Ta đưa đường thẳng d về dạng tổng quát

(d)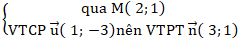

⇒ Phương trình (d) : 3( x - 2) + 1.(y - 1) = 0

Hay ( d) : 3x + y - 7 = 0

Khi đó để hai điểm A và B nằm cùng phía so với đường thẳng d khi và chỉ khi :

(3x_A + y_A - 7)(3x_B + y_B - 7) > 0 ⇔ -2(m - 13) > 0 ⇔ m < 13.

Chọn C.

Ví dụ 7 : Cho đường thẳng d : 3x - 2y + 2 = 0 và ba điểm A( 1 ; 2) ; B( 2 ; -1) ; C(-1 ; -1) . Hỏi đường thẳng d cắt cạnh nào của tam giác BAC ?

A. AB    B. BC    C. AC    D. Không cắt cạnh nào

Lời giải

Đặt f( x ; y) = 3x - 2y + 2.

⇒ f(1 ; 2) = 3.1 - 2.2 + 2 = 1

f(2; -1) = 3.2 - 2.(-1) + 2 = 10

f(-1; -1) = 3.(-1) – 2(-1) + 2 = 1

⇒ f( 1 ; 2).f( 2 ; -1) > 0 nên hai điểm A và B nằm cùng phía so với đường thẳng d.

Tương tự ; hai điểm A và C nằm cùng phía so với đường thẳng d.

Hai điểm B và C nằm cùng phía so với đường thẳng d.

Vậy đường thẳng d không cắt cạnh nào của tam giác ABC.

Chọn D.

C. Bài tập vận dụng

Câu 1: Cho đường thẳng d: x - 5y + 1 = 0 và ba điểm A( 0; -2), B( 1; -3); C(-4; 2). Hỏi đường thẳng d cắt mấy cạnh của tam giác ABC?

A. 0    B. 1    C. 2    D. 3

Lời giải:

Đáp án: C

Trả lời:

Đặt f(x; y) = x - 5y + 1

Suy ra: f( 0; -2) = 0 - 5.(-2) + 1 = 11

f(1; -3) = 1- 5.(-3) + 1 = 17 và f( -4; 2) = - 4 - 5.2 + 1 = - 13

⇒ f( 0; -2) .f( 1; -3) > 0 nên hai điểm A và B nằm cùng phía so với đường thẳng d.

f(0; -2).f( -4; 2) < 0 nên hai điểm A và C nằm khác phía so với đường thẳng d.

f( 1; -3). f(-4; 2)< 0 nên hai điểm B và C nằm khác phía so với đường thẳng d.

Vậy đường thẳng d cắt hai cạnh của tam giác ABC là AC và BC.

Câu 2: Cho đường thẳng d: 3x - 5y + 1 = 0 và hai điểm A( 0; -2); B( 3; 2). Tìm mệnh đề sai.

A. Hai điểm A và B nằm cùng phía so với đường thẳng d.

B. Khoảng cách hai điểm A và B là AB = 5.

C. Đoạn thẳng AB cắt đường thẳng d.

D. Có ít nhất một điểm thuộc đường thẳng d

Lời giải:

Đáp án: A

Trả lời:

+ Khoảng cách hai điểm A và B là: AB = 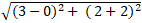= 5

⇒ B đúng .

+ Đặt f( x; y) = 3x - 5y + 1.

⇒ f( 0; -2) = 3.0 - 5.(-2) + 1 = 11

f( 3; 2) = 3.3 - 5.2 + 1 = 0

Suy ra: điểm B thuộc đường thẳng d và đoạn thẳng AB cắt đường thẳng d tại điểm B.

Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: và hai điểm A( 1; 2); B( -3; 4) . Tìm m để d cắt đoạn thẳng AB.

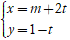
A. m < 3    B. m = 3    C. m > 3    D. Không tồn tại m.

Lời giải:

Đáp án: B

Trả lời:

Ta đưa đường thẳng d về dạng tổng quat

( d) :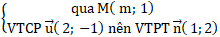

⇒ Phương trình đường thẳng ( d):

1(x - m) + 2( y - 1) = 0 hay x + 2y – m - 2 = 0

Đoạn thẳng AB cắt d khi và chỉ khi một trong hai điểm A; B thuộc đường thẳng ( d) hoặc hai điểm này nằm khác phía so với đường thẳng d

⇔ (x_A + 2y_A - m - 2)(x_B + 2y_B - m - 2) ≤ 0 ⇔ (3 - m)² ≤ 0 ⇔ m = 3

Câu 4: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A( 1; 3);B( - 2; 4) và C(-1; 5) . Đường thẳng d: 2x - 3y + 6 = 0 cắt cạnh nào của tam giác đã cho?

A. Cạnh AC.    B. Cạnh AB.    C. Cạnh BC.    D. Không cạnh nào.

Lời giải:

Đáp án: D

Trả lời:

Đặt f( x; y) = 2x - 3y + 6.

⇒ f[A(1; 3)] = 2.1 - 3.3 + 6 = - 1 < 0

f[ B(-2; 4)] = 2.(-2) – 3.4 + 6 = - 10 < 0

và f[C(- 1; 5)] = 2.(-1) - 3.5 + 6 = -11 < 0

⇒ f(A). f(B) > 0; f(B). f(C) > 0 và f( A).f( C) > 0

⇒ Ba điểm A; B và C nằm cùng phía so với đường thẳng d.

⇒ đường thẳng d không cắt cạnh nào của tam giác ABC.

Câu 5: Cho đường thẳng d: 4x - y + 9 = 0 và ba điểm A( 1; 0); B( -2; 1) và C(-3; 7). Hỏi đường thẳng d cắt cạnh nào của tam giác.

A. AB    B. AC    D. BC    D. Cả ba cạnh.

Lời giải:

Đáp án: D

Trả lời:

Đặt f(x; y) = 4x - y + 9

⇒ f( 1; 0) = 4.1 - 0 + 9 = 13

f(-2; 1) = 4.(-2) - 1 + 9 = 0

và f(-3; 7) = 4.(-3) - 7 + 9 = -10

⇒ Điểm B thuộc đường thẳng d.

Suy ra: cạnh AB cắt đường thẳng d tại B.

Cạnh BC cắt đường thẳng d tại B.

Cạnh AC cắt đường thẳng d vì A và C nằm khác phía so với đường thẳng d.

Câu 6: Cho đường thẳng d: 3x - 4y + 12 = 0 và hai điểm A( -2; 3); B( 3m; -2). Tìm m để đoạn thẳng AB có điểm chung với đường thẳng d.

Lời giải:

Đáp án:

Trả lời:

Để đường thẳng d có điểm chung với đoạn thẳng AB khi và chỉ khi một trong hai điểm A( hoặc B) nằm trên đường thẳng d hoặc hai điểm A; B nằm khác phía so với đường thẳng d.

* Trường hợp 1: Một trong hai điểm A hoặc B thuộc đường thẳng d:

+ Nếu A thuộc đường thẳng d thì: 3.(-2) - 4.3 + 12 = 0 ( vô lí)

⇒ Điểm A không thuộc đường thẳng d.

+ Nếu điểm B thuộc đường thẳng d thì: 3.3m - 4.(-2) + 12 = 0

⇔ 9m + 20 = 0 ⇔ m =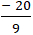

* Trường hợp 2: Hai điểm A và B nằm khác phía so với đường thẳng d.

Đặt f(x; y) = 3x - 4y + 12

⇒ f( -2; 3) = 3.(-2) - 4.3 + 12 = - 6

Và f(3m; - 2) = 3.3m - 4.(-2) + 12 = 9m + 20

Để hai điểm A và B nằm khác phía so với đường thẳng d khi và chỉ khi :

-6(9m+ 20) < 0 ⇔ 9m + 20 > 0

⇔ m >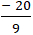

Kết hợp hai trường hợp để đường thẳng d có điểm chung với đoạn thẳng AB thì
m ≥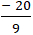

Chú ý: Cách làm nhanh. Cho đường thẳng (d) ax + by + c = 0 và hai điểm A; B. Để đoạn thẳng AB cắt đường thẳng d ( có điểm chung với d) khi và chỉ khi:

( ax_A + by_A + c) .( ax_B + by_B + c) ≤ 0.

Câu 7: Cho đường thẳng d: 7x - y + 2 = 0 và hai điểm A( 1; -3) và B ( 2m; m + 1). Tìm điều kiện của m để đoạn thẳng AB có điểm chung với đường thẳng d?

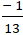
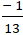
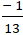
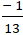
A. m ≤    B. m <    C. m ≥    D. m =

Lời giải:

Đáp án: A

Trả lời:

Đặt f(x; y) = 7x - y + 2

⇒ f(1; -3) = 7.1 - (-3) + 2 = 12

Và f(2m; m + 1) = 7.2m - (m + 1) + 2 = 13m + 1

Để đoạn thẳng AB có điểm chung với đường thẳng d khi và chỉ khi:

12(13m + 1) ≤ 0 ⇔ 13m + 1 ≤ 0

⇔ m ≤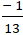

Vậy để đoạn thẳng AB có điểm chung với đường thẳng d thì m ≤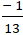

Câu 8: Cho đường thẳng d: 4x - y + 3 = 0 và ba điểm A( -2; 3); B(m + 1; -m - 2);
C( 2m; m + 1). Tìm điều kiện của m để đường thẳng d không cắt cạnh nào của tam giác?

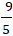
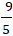
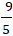
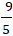
A. m > -    B. m < -    C. m >    D. m <

Lời giải:

Đáp án: B

Trả lời:

+ Đặt f(x; y) = 4x - y + 3

+ Suy ra: f(-2; 3) = 4.(-2) - 3 + 3 = - 8

f( m+1; - m - 2) = 4(m + 1) - (-m - 2) + 3 = 5m + 9

và f(2m; m + 1) = 4.2m - m - 1 + 3 = 7m + 2

+ Để đường thẳng d không cắt cạnh nào của tam giác ABC khi và chỉ khi ba điểm A; B và C nằm cùng phía so với đường thẳng d:

⇔

⇔

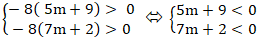
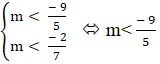
Vậy để đường thẳng d không cắt cạnh nào của tam giác ABC thì m < -