Viết phương trình đường tròn biết tâm, bán kính, đường kính - Toán lớp 10

---

Viết phương trình đường tròn biết tâm, bán kính, đường kính

Với Viết phương trình đường tròn biết tâm, bán kính, đường kính Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình đường tròn biết tâm, bán kính, đường kính từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Phương pháp giải

+ Đường tròn ( C) : tâm I (a; b) và bán kính R có phương trình :

(x - a)² + (y - b)² = R²

+ Cho hai điểm A(x_A; y_A) và B(x_B; y_B). Để viết phương trình đường tròn đường kính AB ta làm như sau:

- Bước 1: Tìm trung điểm I của AB.

- Bước 2: Tính IA.

- Bước 3: Lập phương trình đường tròn ( C) tâm I và bán kính R = IA.

+ Đường tròn ( C) tâm I và đi qua điểm A

⇒ Đường tròn ( C): tâm I và bán kính R = IA.

B. Ví dụ minh họa

Ví dụ 1. Cho hai điểm A( 5; -1) ; B( -3; 7) . Đường tròn có đường kính AB có phương trình là

A. x² + y² + 2x - 6y - 22 = 0.    B. x² + y² - 2x - 6y - 22 = 0.

C. x² + y² - 2x - y + 1 = 0.    D. Tất cả sai

Lời giải

Tâm I của đường tròn là trung điểm AB nên I( 1; 3) .

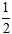
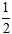
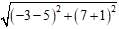
Bán kính R = AB = = 4√2

Vậy phương trình đường tròn là: (x - 1)² + (y - 3)² = 32

Hay x² + y² - 2x- 6y - 22 = 0.

Chọn B.

Ví dụ 2. Cho hai điểm A( -4; 2) và B(2; -3). Tập hợp điểm M thỏa mãn có phương trình là

A. x² + y² + 2x + 6y + 1= 0.    B. x² + y² - 6x - y + 1 = 0.

C. x² + y² - 2x - 6y – 10 = 0.    D. x² + y² + 2x + y + 1 = 0.

Lời giải

Ta có: MA→(x + 4;y - 2); MB→(x - 2; y + 3)

Theo giả thiết: MA² + MB² = 31

Tương đương : ( x + 4)² + (y - 2)² + (x - 2)² + (y + 3)² = 31

Hay x² + y² + 2x + y + 1 = 0

Chọn D.

Ví dụ 3. Đường tròn tâm I( 3; -2) và bán kính R= 2 có phương trình là

A. ( x + 3)² + (y + 2)² = 2    B. (x - 3)² + (y + 2)² = 4

C. ( x + 3)² + (y - 2)² = 4    D. (x - 3)² + (y - 2)² = 4

Lời giải

Phương trình đường tròn có tâm (3; -2) , bán kính R = 2 là:

(x - 3)² + (y + 2)² = 4

Chọn B.

Ví dụ 4. Đường tròn tâm I( -1; 2) và đi qua điểm M( 2;1) có phương trình là

A. x² + y² + 2x + 4y - 5 = 0.    B. x² + y² + 2x - 4y - 5 = 0.

C. x² + y² + 2x + 4y + 5 = 0.    D. x² + y² - 2x + 4y - 5 = 0.

Hướng dẫn giải

Đường tròn có tâm I( -1; 2) và đi qua M( 2; 1) thì có bán kính là:

R = IM = 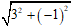= √10

Khi đó có phương trình là: (x + 1)² + ( y - 2)² = 10

Hay x² + y² + 2x - 4y - 5 = 0.

Chọn B.

Ví dụ 5. Cho hai điểm A( 5; -1) và B( -3; 7). Đường tròn có đường kính AB có phương trình là

A. x² + y² - 2x + 6y - 3 = 0.    B. x² +y² - 2x - 6y - 22 = 0

C. x² +y² + 2x + 6y - 3 = 0    D. x² +y² + 2x + 6y - 15 = 0

Hướng dẫn giải

Tâm I của đường tròn là trung điểm của AB nên I( 1;3) .

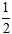
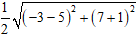
Bán kính AB = = 4√2

Vậy phương trình đường tròn là:

(x - 1)² + (y - 3)² = 32 hay x² +y² - 2x - 6y - 22 = 0

Chọn B.

Ví dụ 6: Lập phương trình đường tròn đi qua điểm A(3; 1); B(5; 5) và tâm I nằm trên trục hoành?

A.(x - 1)² + y² = 16    B. (x - 10)² + y² = 50

C. (x + 1)² + y² = 17    D. (x - 10)² + y² = 50

Lời giải

+ Tâm I của đường tròn nằm trên trục hoành nên I(a; 0).

⇒ Phương trình đường tròn ( C): (x - a)² + y² = R².

+ Điểm A( 3; 1) thuộc (C) nên (3 - a)² + 1² = R² (1).

+ Điểm B( 5; 5) thuộc ( C) nên ( 5 - a)² + 5² = R² ( 2).

Lấy (1) trừ (2); vế trừ vế ta được : 4a - 40 = 0

⇔ 4a = 40 ⇔ a = 10

Thay a = 10 vào (1) ta được: R² = 50.

Vậy phương trình đường tròn ( C): (x - 10)² + y² = 50

Chọn D.

Ví dụ 7: Lập phương trình đường tròn đi qua điểm A(0; 1); B(1; 0) và tâm I nằm trên đường thẳng d: x + y + 2 = 0?

A. x² + y² - 2x + 2y - 1 = 0    B. x² + y² + 2x + 2y - 3 = 0

C. x² + y² + 4x - 3 = 0    D. Tất cả sai

Lời giải

Giả sử phương trình đường tròn ( C): x² + y² - 2ax - 2by + c = 0 ( với a² + b² - c > 0)

Là đường tròn có tâm I(a; b).

+ Do điểm A(0; 1) thuộc đường tròn nên: 0 + 1 - 2b + c = 0 hay – 2b + c = - 1 (1)

+ Do điểm B(1; 0) thuộc đường tròn nên: 1 + 0 - 2a + c = 0 hay -2a + c = -1 (2)

+ Do tâm I thuộc đường thẳng d: x + y + 2 = 0 nên a + b + 2 = 0 (3).

Từ ( 1); (2) và (3) ta có hệ phương trình :

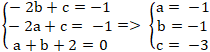
⇒ Phương trình đường tròn cần tìm là:

x² + y² + 2x + 2y - 3 = 0

Chọn B.

C. Bài tập vận dụng

Câu 1: Đường tròn tâm I ( 3; -1) và bán kính R = 2 có phương trình là

A. (x + 3)² + (y - 1)² = 4.    B. (x - 3)² + (y - 1)² = 4.

C. (x - 3)² + (y + 1)² = 4.    D. (x + 3)² + (y + 1)² = 4.

Lời giải:

Đáp án: C

Trả lời:

Phương trình đường tròn có tâm I( 3; -1) , bán kính R = 2 là:

(x - 3)² + (y + 1)² = 4

Câu 2: Đường tròn tâm I( -1; 2) và đi qua điểm M( 2; 1) có phương trình là

A. x² + y² + 2x - 4y - 5 = 0    B. x² + y² + 2x - 4y - 3 = 0

C. x² + y² - 2x - 4y - 5 = 0    D. x² + y² + 2x + 4y - 5 = 0

Lời giải:

Đáp án: A

Trả lời:

+ Đường tròn có tâm I( -1; 2) và đi qua M(2; 1) thì có bán kính là:

R = IM = 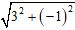= √10

+ Khi đó đường tròn có phương trình là:

(x + 1)² + (y - 2)² = 10 ⇔ x² + y² + 2x - 4y - 5 = 0

Câu 3: Đường tròn tâm I( 1; 4) và đi qua điểm B( 2; 6) có phương trình là

A. (x + 1)² + (y + 4)² = 5    B. (x - 1)² + (y - 4)² = √5

C. (x + 1)² + (y + 4)² = √5    D. (x - 1)² + (y - 4)² = 5

Lời giải:

Đáp án: D

Trả lời:

Đường tròn có tâm I( 1; 4) và đi qua B( 2; 6) thì có bán kính là:

R = IB = 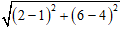= √5

Khi đó đường tròn có phương trình là: (x - 1)² + (y - 4)² = 5

Câu 4: Cho điểm M( x ; y) có 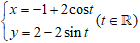. Tập hợp điểm M là

A. Đường tròn tâm I (-1 ;2) và R = 3.    B. Đường tròn tâm I(-1 ; 2) và R = 2.

C. Đường tròn tâm I(-1 ; 2) và R = 4.    D. Đường tròn tâm I(1; -2) và R = 4.

Lời giải:

Đáp án: B

Trả lời:

Ta có: M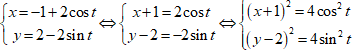

⇒ (x + 1)² + (y - 2)² = 4cos²t + 4sin²t ⇔ (x + 1)² + (y - 2)² = 4(sin²t + cos²t)

⇔ (x + 1)² + (y - 2)² = 4

Vậy tập hợp điểm M là phương trình đường tròn có tâm I ( -1; 2) , bán kính R = 2.

Câu 5: Cho hai điểm A( 5; -1) ; B( -3; 7) . Đường tròn có đường kính AB có phương trình là

A. x² + y² - 2x - 6y - 22 = 0    B. x² + y² - 2x - 6y + 22 = 0

C. x² + y² - 2x - y - 1 = 0    D. x² + y² + 6x + 5y + 1 = 0

Lời giải:

Đáp án: A

Trả lời:

Đường tròn ( C) có đường kính AB nên tâm I của đường tròn là trung điểm AB

⇒ Tọa độ điểm I : 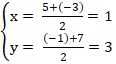⇒ I( 1; 3)

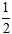
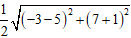
Bán kính R = AB = = 4√2

Vậy phương trình đường tròn là:

(x - 1)² + (y - 3)² = 32 ⇔ x² + y² - 2x - 6y - 22 = 0

Câu 6: Cho hai điểm A( - 4; 2) và B( 2; -3) . Tập hợp điểm M(x; y) thỏa mãn :
MA² + MB² = 31 có phương trình là

A. x² + y² + 2x + 6y + 1 = 0    B. x² + y² - 6x - 5y + 1 = 0

C. x² + y² - 2x - 6y - 22 = 0    D. x² + y² + 2x + y + 1 = 0

Lời giải:

Đáp án: D

Trả lời:

Ta có: MA² = ( x + 4)² + (y - 2)² và MB² = ( x - 2)² + (y + 3)²

Để MA² + MB² = 31

⇔ (x + 4)² + (y - 2)² + (x - 2)² + (y + 3)² = 31 ⇔ x² + y² + 2x + y + 1 = 0

Câu 7: Lập phương trình đường tròn đi qua hai điểm A(1; 2); B(2; 1) và tâm nằm trên đường thẳng (d): 3x + 4y + 7 = 0?

A. x² + y² + 2x + 2y - 11 = 0     B. x² + y² – 2x + 2y - 11 = 0

C. x² + y² + 2x - 2y - 11 = 0    D. x² + y² – 2x - 2y – 11 = 0

Lời giải:

Đáp án: A

Trả lời:

+ Gọi phương trình đường tròn cần tìm ( C): x² + y² - 2ax - 2by + c = 0 (a² + b² - c > 0).

Đường tròn này có tâm I(a;b).

+ Do tâm I nằm trên đường thẳng d: 3x + 4y + 7 = 0 nên 3a + 4b + 7 = 0 (1).

+ Do điểm A(1;2) nằm trên đường tròn nên:

1 + 4 - 2a - 4b + c = 0 hay -2a - 4b + c = - 5 (2)

+ Do điểm B(2;1) nằm trên đường tròn nên :

4 + 1 - 4a - 2b + c = 0 hay – 4a - 2b + c = -5 (3)

Từ (1); (2) và (3) ta có hệ:

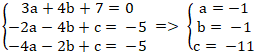
⇒ Phương trình đường tròn cần tìm là:

x² + y² + 2x + 2y - 11 = 0

Câu 8: Biết đường tròn ( C) đi qua A(1; 2); B(3; 1) và tâm I nằm trên trục tung. Tìm tâm đường tròn?

A. I(0; -2)    B. I( 0; 1)    C. I(0; 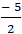)    D. I(0; )

Lời giải:

Đáp án: C

Trả lời:

+ Do tâm I đường tròn nằm trên trục tung nên I(0; a).

⇒ Phương trình đường tròn có dạng: x² + (y - a)² = R²

+ Điểm A( 1; 2) thuộc đường tròn ( C) nên :

12 + (2 - a)² = R² hay a² - 4a - R² = - 5 (1)

+ Điểm B(3; 1) thuộc đường tròn (C) nên :

32 + (1 - a)² = R² hay a² – 2a – R² = - 10 (2)

+ Lấy (1) trừ (2) vế trừ vế ta được:

- 2a = 5 ⇔ a =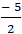

⇒ Tâm đường tròn là I(0; )