Cho mạch điện như hình vẽ. Biết UAB = 90 V; R1 = R3 = 45Omega ; R2 = 90Omega. Tìm R4. Biết khi K mở và khí K đóng cường độ dòng điện qua R4 là như nhau.

Câu hỏi:

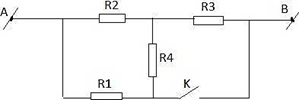
Trả lời:

Lời giải

- Khi K mở mạch trở thành: (R₂ // (R₁ nt R₄)) nt R₃

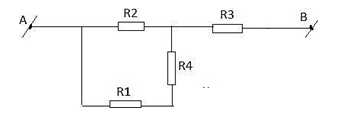
R₁₄ = R₁ + R₄ = 45 + R₄

\({R_{124}} = \frac{{{R_2}.\left( {45 + {R_4}} \right)}}{{{R_2} + 45 + {R_4}}} = \frac{{90\left( {45 + {R_4}} \right)}}{{135 + {R_4}}}\)

\({R_{1234}} = {R_3} + {R_{124}} = 45 + \frac{{90\left( {45 + {R_4}} \right)}}{{135 + {R_4}}} = \frac{{10125 + 135{R_4}}}{{135 + {R_4}}}\)

Lại có:

I = I₃ = I₁₂₄ = \(\frac{{{U_{AB}}}}{{R{}_{1234}}} = \frac{{90\left( {135 + {R_4}} \right)}}{{10125 + 135{R_4}}}\)

I₁₂₄ = I₂ + I₁₄ \( \Rightarrow {I_1} = {I_4} = {I_{14}} = {I_{124}} - {I_2}\)

Mà U₂ = U₁₄ = U₁₂₄

Nên \({I_4} = {I_{124}} - \frac{{{U_{124}}}}{{{R_2}}} = {I_{124}} - \frac{{{I_{124}}.{R_{124}}}}{{{R_2}}} = {I_{124}}\left( {1 - \frac{{{R_{124}}}}{{{R_2}}}} \right)\)

\[ \Rightarrow {I_4} = \frac{{90\left( {135 + {R_4}} \right)}}{{10125 + 135{R_4}}}\left( {1 - \frac{{90\left( {45 + {R_4}} \right)}}{{\left( {135 + {R_4}} \right).90}}} \right)\]

\( \Rightarrow {I_4} = \frac{{8100}}{{10125 + 135{R_4}}} = \frac{{180}}{{225 + 3{R_4}}}\) (1)

- Khi K đóng mạch trở thành: R­₁ // (R₂ nt (R₃ //R₄))

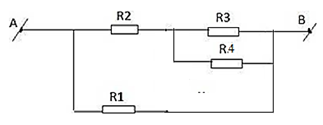
\({R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\)

\({R_{234}} = {R_2} + {R_{34}} = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\)

\({R_{1234}} = \frac{{{R_1}.{R_{234}}}}{{{R_1} + {R_{234}}}} = \frac{{45.\left( {4050 + 135{R_4}} \right)}}{{\left( {45 + {R_4}} \right).\left( {45 + \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}} \right)}} = \frac{{4050 + 135{R_4}}}{{135 + 4{R_4}}}\)

Ta có: U_AB = U₂₃₄ = U₁; U₂₃₄ = U₂ + U₃₄; U₃₄ = U₃ = U₄

Nên \({I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{{{U_{34}}}}{{{R_4}}} = \frac{{{U_{234}} - {U_2}}}{{{R_4}}} = \frac{{{U_{AB}} - {U_2}}}{{{R_4}}} = \frac{{{U_{AB}} - {I_2}.{R_2}}}{{{R_4}}}\)

Mà I₂ = I₂₃₄ = \(\frac{{{U_{234}}}}{{{R_{234}}}} = \frac{{{U_{AB}}}}{{{R_{234}}}}\)

\( \Rightarrow {I_4} = \frac{{{U_{A{\bf{B}}}} - \frac{{{U_{AB}}}}{{{R_{234}}}}.{R_2}}}{{{R_4}}} = \frac{{90 - \frac{{90.90}}{{{R_{234}}}}}}{{{R_4}}} = \frac{{90{R_{234}} - 8100}}{{{R_4}.{R_{234}}}}\) (*)

Thay R₂₃₄= \(\frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\) vào (*) ta được:

\({I_4} = \frac{{4050}}{{4050 + 135{R_4}}}\) (2)

Vì I₄ trong 2 trường hợp là bằng nhau nên (1) = (2)

\(\frac{{180}}{{225 + 3{R_4}}}\)\( = \frac{{4050}}{{4050 + 135{R_4}}}\)\( \Rightarrow \frac{6}{{75 + {R_4}}} = \frac{{135}}{{1350 + 45{R_4}}}\)

\( \Rightarrow 8100 + 270{R_4} = 10125 + 135{R_4} \Rightarrow {R_4} = 15\Omega \)