Cho mạch điện: U = 16V , R0 =4 Ω , R1 = 12 Ω, Rx là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể. 1. Tính Rx sao cho công suất tiêu thụ trên nó bằ
Câu hỏi:
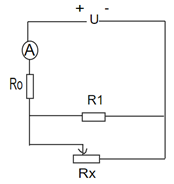
Cho mạch điện: U = 16V , R0 =4 Ω , R1 = 12 Ω, Rx là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.
1. Tính Rx sao cho công suất tiêu thụ trên nó bằng 9 W và tính hiệu suất của mạch điện. Biết rằng tiêu hao năng lượng trên R1, Rx là có ích, trên R0 là vô ích.
2. Với giá trị nào của Rx thì công suất tiêu thụ trên nó là cực đại? Tính công suất ấy?
Trả lời:
Lời giải
Mạch: \({R_0}nt\left( {{R_1}//R{}_x} \right)\)
Đặt Rx = x \(\left( \Omega \right)\)
\({R_{td}} = {R_0} + \frac{{{R_1}.x}}{{{R_1} + x}} = 4 + \frac{{12x}}{{12 + x}} = \frac{{16x + 48}}{{12 + x}}\)
\( \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{16}}{{\frac{{16x + 48}}{{12 + x}}}} = \frac{{12 + x}}{{x + 3}}\)
\({U_{Rx}} = U{}_{R1} = U{}_{R1x} = \frac{{12 + x}}{{x + 3}}.\frac{{12x}}{{12 + x}} = \frac{{12x}}{{x + 3}}\)
Mà \(P = \frac{{U_{Rx}^2}}{{{R_x}}} = 9W \Leftrightarrow \frac{{\frac{{144{x^2}}}{{{{\left( {x + 3} \right)}^2}}}}}{x} = 9 \Rightarrow 9{x^2} - 90x + 81 = 0\)
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow {R_x} = 1\left( \Omega \right)}\\{x = 9 \Rightarrow {R_x} = 9\left( \Omega \right)}\end{array}} \right.\)
Hiệu suất của mạch điện
\(H = \frac{{{P_{1x}}}}{P}.100\% = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.{R_{td}}}}.100\% = \frac{{{R_{1x}}}}{{{R_{td}}}}.100\% = \frac{{3{R_x}}}{{4{R_x} + 12}}.100\% \)
+ Rx = 1\(\left( \Omega \right)\) \( \Rightarrow H = 18,75\% \)
+ Rx = 9\(\left( \Omega \right)\) \( \Rightarrow H = 56,25\% \)
b. Từ câu a
\( \Rightarrow {P_{{R_x}}} = \frac{{{U^2}}}{{{R_x}}} = \frac{{{{\left( {\frac{{12x}}{{x + 3}}} \right)}^2}}}{x} = \frac{{144x}}{{{x^2} + 6x + 9}} = \frac{{144}}{{x + \frac{9}{x} + 6}}\)
Để PRx max khi \((x + \frac{9}{x} + 6)\,\,\min \)\( \Rightarrow \left( {x + \frac{9}{x}} \right)\,\,\min \)
Áp dụng BĐT Cô – si: \(x + \frac{9}{x} \ge 2\sqrt {x.\frac{9}{x}} = 6\)
\( \Rightarrow {P_{Rx\,max}} = \frac{{144}}{{6 + 6}} = 12\,\left( W \right)\)