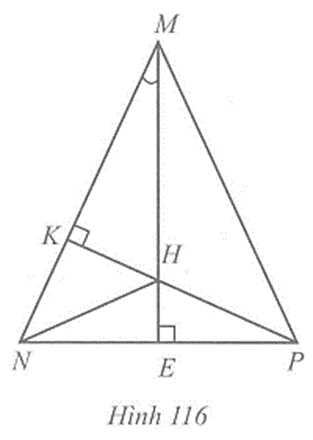
Cho tam giác nhọn MNP có trực tâm H. Khi đó góc HMN bằng góc nào

Cho tam giác nhọn MNP có trực tâm H. Khi đó góc HMN bằng góc nào sau đây?

Giải vở bài tập Toán 7 Bài tập cuối chương 7

Câu 12 trang 130 vở bài tập Toán lớp 7 Tập 2: Cho tam giác nhọn MNP có trực tâm H. Khi đó góc HMN bằng góc nào sau đây?

A. Góc HPN ;

B. Góc NMP;

C. Góc MPN;

D. Góc NHP.

Lời giải:

Vẽ đường cao ME, PK của tam giác MNP.

Xét tam giác MNE vuông tại E, ta có:

$\widehat{EMN}$ + $\widehat{MNE}$ = 90^o (tổng hai góc nhọn trong tam giác vuông)

Hay $\widehat{HMN}$ + $\widehat{MNP}$ = 90^o (1)

Xét tam giác NPK vuông tại K, ta có

$\widehat{KPN}$ + $\widehat{KNP}$ = 90^o (tổng hai góc nhọn trong tam giác vuông)

Hay $\widehat{HPN}$ + $\widehat{MNP}$ = 90^o (2)

Từ (1) và (2) suy ra $\widehat{HMN}$ = $\widehat{HPN}$.

- Vì tia MH nằm trong góc NMP nên $\widehat{HMN}$ < $\widehat{NMP}$

- Vì tia PH nằm trong góc MPN nên $\widehat{HPN}$ < $\widehat{MPN}$ hay $\widehat{HMN}$ < $\widehat{MPN}$.

- Xét tam giác NHK vuông tại K, ta có $\widehat{NHK}$ + $\widehat{KNH}$ = 90^o (tổng hai góc nhọn trong tam giác vuông). Suy ra $\widehat{NHK}$ < 90^o.

Mà $\widehat{NHK}$ + $\widehat{NHP}$ = 180^o (hai góc kề bù). Suy ra $\widehat{NHP}$ > 90^o.

Từ (1) suy ra $\widehat{HMN}$ < 90^o. Do đó $\widehat{HMN}$ < $\widehat{NHP}$.

Vậy ta chọn đáp án A.