Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM

Cho hai tam giác ABC và MNP có:

Giải vở bài tập Toán 7 Bài tập cuối chương 7

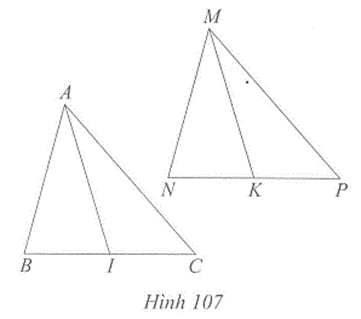
Câu 4 trang 124 vở bài tập Toán lớp 7 Tập 2: Cho hai tam giác ABC và MNP có:

AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh AI = MK.

Lời giải:

Xét hai tam giác ABC và MNP, ta có:

AB = MN, BC = NP, CA = PM

Suy ra ∆ABC = ∆MNP (c.c.c)

Do đó $\hat{B}$ = $\hat{N}$ (hai góc tương ứng)

Vì I là trung điểm của BC nên BI = $\frac{1}{2}$BC

Vì K là trung điểm của NP nên NK = $\frac{1}{2}$NP

Mà BC = NP, suy ra BI = NK

Xét hai tam giác ABI và MNK, ta có:

AB = MN, $\hat{B}$ = $\hat{N}$ ; BI = NK

Suy ra ∆ABI = ∆MNK (c.g.c)

AI = MK (hai cạnh tương ứng)