Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C
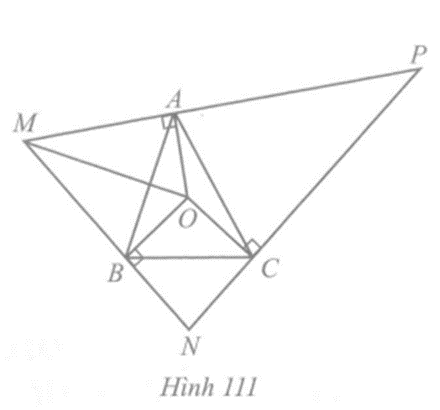
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc OA, OB, OC hai đường trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 111). Chứng minh:
Giải vở bài tập Toán 7 Bài tập cuối chương 7
Câu 8 trang 127 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc OA, OB, OC hai đường trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 111). Chứng minh:
a) ∆OMA = ∆OMB và tia Om là tia phân giác của góc NMP;
b) O là giao điểm của ba đường phân giác của tam giác MNP.
Lời giải:
Xét hai tam giác vuông OMA và OMB, ta có:
OM là cạnh chung;
OA = OB (vì O là giao điểm ba đường trung trực của tam giác ABC).
Suy ra ∆OMA = ∆OMB (cạnh huyền – cạnh góc vuông).
Do đó = (hai góc tương ứng).
Vậy tia OM là tia phân giác của góc MNP.
b) Xét hai tam giác vuông ONB và ONC, ta có:
ON là cạnh chung;
OB = OC (vì O là giao điểm ba đường trung trực của tam giác ABC).
Suy ra ∆ONB = ∆ONC (cạnh huyền – cạnh góc vuông).
Do đó = (hai góc tương ứng).
Vậy NO là tia phân giác của góc MNP.
Tam giác MNP có MO là tia phân giác của góc NMP, NO là tia phân giác của góc MNP nên O là giao điểm ba đường phân giác của tam giác MNP.