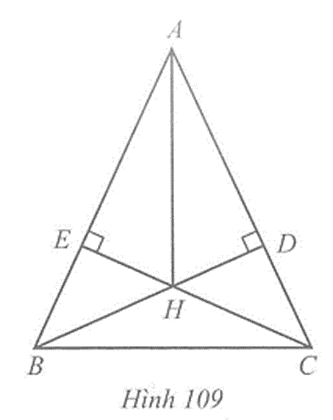
Cho tam giác ABC cân tại A có góc ABC = 70 độ, Hai đường thẳng BD và CE cắt nhau tại H

Cho tam giác ABC cân tại A có = 70. Hai đường thẳng BD và CE cắt nhau tại H.

Giải vở bài tập Toán 7 Bài tập cuối chương 7

Câu 6 trang 126 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có $\widehat{ABC}$ = 70^o. Hai đường thẳng BD và CE cắt nhau tại H.

a) Tính số đo các góc còn lại của tam giác ABC;

b) Chứng minh BD = CE;

c) Chứng minh tia AH là tia phân giác của góc BAC.

Lời giải:

Vì tam giác ABC cân tại A nên $\widehat{ACB}$ = $\widehat{ABC}$

Mà $\widehat{ABC}$ = 70^o nên $\widehat{ACB}$ = 70^o

Do $\widehat{BAC}$ + $\widehat{ABC}$ + $\widehat{ACB}$ = 180^o (tổng ba góc của một tam giác)

Nên $\widehat{BAC}$ = 180^o – ( $\widehat{ABC}$ + $\widehat{ACB}$ ) = 180^o – (70^o + 70^o) = 40^o.

b) Xét hai tam giác vuông ABD và ACE, ta có

AB = AC (hai cạnh bên của tam giác cân); $\hat{A}$ là góc chung

Suy ra ∆ABD = ∆ACE (cạnh huyền – góc nhọn)

Do đó BD = CE (hai cạnh tương ứng)

c) Ta có ∆ABD = ∆ACE nên AD = AE (hai cạnh tương ứng)

Xét hai tam giác vuông ADH và AEH, ta có:

AH là cạnh chung; AD = AE

Suy ra ∆ADH = ∆AEH (cạnh huyền – cạnh góc vuông)

Do $\widehat{HAD}$ = $\widehat{HAE}$ (hai góc tương ứng)

Vậy AH là tia phân giác của góc BAC.