Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
Giải vở bài tập Toán 7 Bài tập cuối chương 7
Câu 9 trang 128 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng;
b) Nếu ba điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Lời giải:
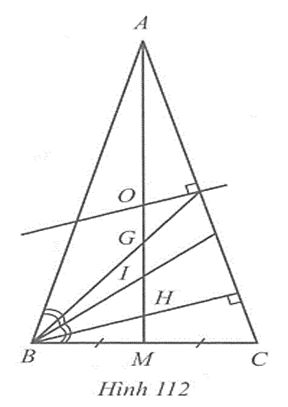
a) Hình 112
Vẽ đường trung tuyến AM của tam giác ABC. Suy ra G thuộc đường thẳng AM.
Xét hai tam giác ABM và ACM, ta có
AM là cạnh chung;
AB = AC (hai cạnh bên của tam giác cân);
MB = MC (vì M là trung điểm của BC).
Suy ra ∆ABM = ∆ACM (c.c.c).
Do đó = và = (hai góc tương ứng).
Ta có + = 180o (hai góc kề bù) và = nên và = = 90o hay AM BC. Suy ra điểm H thuộc đường thẳng AM.
Do = nên AM là tia phân giác của góc BAC. Suy ra điểm I thuộc đường thẳng AM.
Do AB = AC và MB = MC nên AM là đường trung trực của cạnh BC. Suy ra điểm O thuộc đường thẳng AM.
Như vậy, các điểm G, H, I, O thuộc đường thẳng AM hay các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
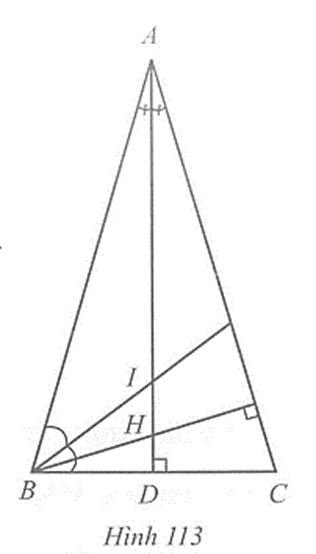
b) Hình 113
Vẽ đường cao AD của tam giác ABC. Do các điểm A, H, I cùng nằm trên một đường thẳng nên AD là đường phân giác của tam giác ABC.
Xét hai tam giác vuông ABD và ACD, ta có:
AD là cạnh chung;
= (vì AD là tia phân giác của góc BAC).
Suy ra ∆ABD = ∆ACD (cạnh góc vuông – góc nhọn).
Do đó AB = AC (hai cạnh tương ứng).
Vậy tam giác ABC là tam giác cân.