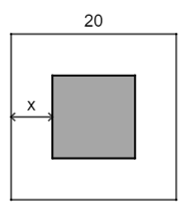
Trên một khu vườn hình vuông có cạnh bằng 20 m người ta làm một lối đi xung quanh vườn có bề rộng x (m)
Trên một khu vườn hình vuông có cạnh bằng 20 m người ta làm một lối đi xung quanh vườn có bề rộng x (m) (Hình dưới). Để diện tích lối đi là 76 m2 thì bề rộng x là bao nhiêu?
Giải vở thực hành Toán 9 Bài 4: Phương trình quy về phương trình bậc nhất một ẩn - Kết nối tri thức
Bài 8 trang 35 VTH Toán 9 Tập 1: Trên một khu vườn hình vuông có cạnh bằng 20 m người ta làm một lối đi xung quanh vườn có bề rộng x (m) (Hình dưới). Để diện tích lối đi là 76 m2 thì bề rộng x là bao nhiêu?
Lời giải:
Phần đất làm vườn là hình vuông có cạnh 20 – 2x (m) và có diện tích là (20 – 2x)2 (m2).
Theo giả thiết, diện tích đất dành cho làm vườn là 202 – 76 = 400 – 76 = 324 suy ra (20 – 2x)2 = 324 = 182 hay (20 – 2x)2 – 182 = 0 (1).
Giải phương trình (1): (20 – 2x)2 – 182 = 0
(20 – 2x – 18)(20 – 2x + 18) = 0
(2 – 2x)(38 – 2x) = 0.
Suy ra 2 – 2x = 0 hoặc 38 – 2x = 0.
• 2 – 2x = 0 hay 2x = 2, suy ra x = 1.
• 38 – 2x = 0 hay 2x = 38, suy ra x = 19 (loại vì 20 – 2.19 = −18 < 0).
Vậy bề rộng của lối đi là 1 m.
Lời giải vở thực hành Toán 9 Bài 4: Phương trình quy về phương trình bậc nhất một ẩn hay khác:
Câu 2 trang 30 VTH Toán 9 Tập 1: Chọn phương án đúng. Nghiệm của phương trình x2 – 16 = 0 là...
Câu 3 trang 30 VTH Toán 9 Tập 1: Chọn phương án đúng. Điều kiện xác định của phương trình là ...
Câu 4 trang 31 VTH Toán 9 Tập 1: Chọn phương án đúng. Nghiệm của phương trình là ...
Bài 1 trang 31 VTH Toán 9 Tập 1: Giải các phương trình sau: x(x – 2) = 0; (2x + 1)(3x – 2) = 0....