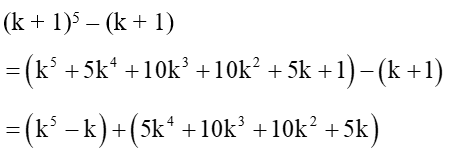Bài 9 trang 38 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 2: Nhị thức newton

Haylamdo biên soạn và sưu tầm lời giải Bài 9 trang 38 Chuyên đề Toán 10 trong Bài 2: Nhị thức newton. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 9 trang 38 Chuyên đề Toán 10: Bằng phương pháp quy nạp, chứng minh:

a) n⁵ – n chia hết cho 5 ∀ n ∈ ℕ^*;

b) n⁷ – n chia hết cho 7 ∀ n ∈ ℕ^*.

Lời giải:

a)

+) Với n = 1, ta có: 1⁵ – 1 = 0 ⁝ 5.

Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)⁵ – (k + 1) ⁝ 5.

Thật vậy, theo giả thiết quy nạp ta có: k⁵ – k ⁝ 5.

Khi đó:

Mà (k⁵ - k) và (5k⁴ + 10k³ + 10k² + 5k) đều chia hết cho 5, do đó

(k⁵ - k) + (5k⁴ + 10k³ + 10k² + 5k) ⁝ 5 hay (k + 1)⁵ – (k + 1) ⁝ 5.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ^*.

b)

+) Với n = 1, ta có: 1⁷ – 1 = 0 ⁝ 7.

Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)⁷ – (k + 1) ⁝ 7.

Thật vậy, theo giả thiết quy nạp ta có: k⁷ – k ⁝ 7.

Khi đó:

(k + 1)⁷ – (k + 1)

= (k⁷ + 7k⁶ + 21k⁵ + 35k³ + 21k² + 7k +1) - (k+ 1)

= (k⁷ - k) + (7k⁶ + 21k⁵ + 35k³ + 21k² + 7k)

Mà (k⁷ - k) và (7k⁶ + 21k⁵ + 35k³ + 21k² + 7k) đều chia hết cho 7, do đó

(k⁷ - k) + (7k⁶ + 21k⁵ + 35k³ + 21k² + 7k) ⁝ 7 hay (k + 1)⁷ – (k + 1) ⁝ 7.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ^*.