Bài 5 trang 41 Chuyên đề Toán 11 Chân trời sáng tạo
Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 1 - Chân trời sáng tạo
Bài 5 trang 41 Chuyên đề Toán 11: Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
A. Không có.
B. Một.
C. Hai.
D. Vô số.
Lời giải:
Đáp án đúng là: B
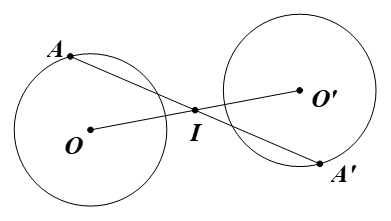
Giả sử (H) là hình gồm hai đường tròn phân biệt có cùng bán kính (O; R) và (O’; R).
Gọi I là trung điểm của đoạn OO’.
Suy ra O’ = ĐI(O).
Gọi A là điểm bất kì trên (O; R).
Lấy điểm A’ sao cho I là trung điểm của AA’. Khi đó A’ = ĐI(A).
Dễ dàng chứng minh được DOAI = DO’A’I (c.g.c)
Suy ra OA = O’A’ (hai cạnh tương ứng)
Mà OA = R nên O’A’ = R hay A’ nằm trên (O’; R).
Khi đó ta luôn xác định được một điểm A’ trên hình (H) sao cho A’ = ĐI(A).
Tương tự như vậy, ta chọn các điểm khác bất kì trên hình (H), ta đều xác định được ảnh của các điểm đó qua ĐI trên hình (H).
Vì vậy I là tâm đối xứng của hình (H).
Với mỗi điểm M bất kì sao cho M ≠ I, ta luôn có MO ≠ MO’.
Do đó O’ không phải là ảnh của O qua ĐM.
Vậy hình gồm hai đường tròn phân biệt có cùng bán kính có 1 tâm đối xứng duy nhất là trung điểm của đoạn nối tâm.
Do đó ta chọn phương án B.
Lời giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 1 hay, chi tiết khác: