Bài 6 trang 36 Chuyên đề Toán 11 Chân trời sáng tạo

Giải Chuyên đề Toán 11 Bài 6: Phép vị tự - Chân trời sáng tạo

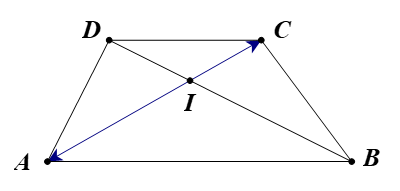
Bài 6 trang 36 Chuyên đề Toán 11: Cho hình thang ABCD có hai đáy là AB và CD với $CD = \frac{1}{2} AB$ . Gọi I là giao điểm của hai đường chéo AC và BD. Tìm phép vị tự biến $\vec{AB}$ thành $\vec{CD}$ .

Lời giải:

Vì ABCD là hình thang nên AB // CD

Ta có I là giao điểm của hai đường chéo AC và BD, áp dụng hệ quả định lí Thales, ta được $\frac{IC}{IA} = \frac{IB}{ID} = \frac{CD}{AB} = \frac{1}{2}$ .

Suy ra $IC = \frac{1}{2} IA$ .

Mà A, C nằm khác phía so với I.

Do đó $\vec{IC} = - \frac{1}{2} \vec{IA}$ .

Vì vậy $V_{(I, - \frac{1}{2})} (A) = C$ .

Chứng minh tương tự, ta được $V_{(I, - \frac{1}{2})} (B) = D$ .

Khi đó qua phép vị tự $V_{(I, - \frac{1}{2})}$ biến $\vec{AB}$ thành $\vec{CD}$ .

Vậy phép vị tự cần tìm là $V_{(I, - \frac{1}{2})}$ .

Lời giải Chuyên đề Toán 11 Bài 6: Phép vị tự hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯