Bài 8 trang 36 Chuyên đề Toán 11 Chân trời sáng tạo

Giải Chuyên đề Toán 11 Bài 6: Phép vị tự - Chân trời sáng tạo

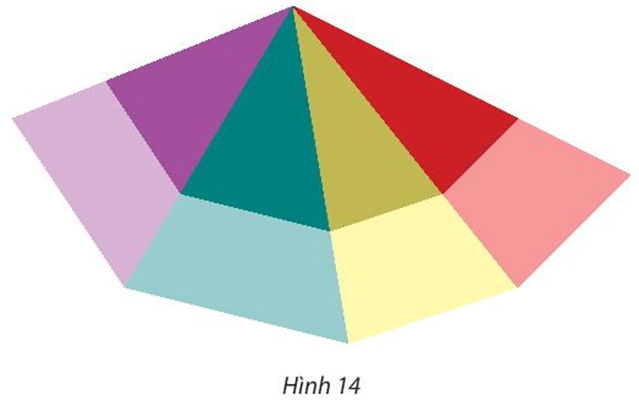
Bài 8 trang 36 Chuyên đề Toán 11: Trong Hình 14, tìm phép vị tự được dùng để biến bốn tam giác nhỏ thành bốn tam giác lớn.

Bài 8 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Lời giải:

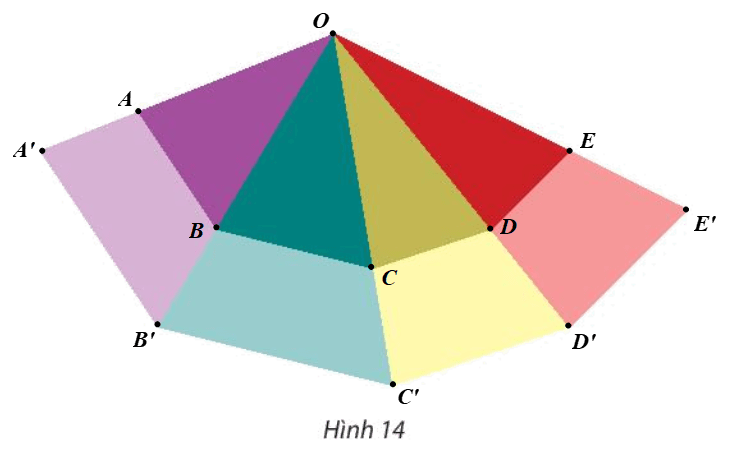
Giả sử ta chọn điểm O như hình vẽ.

Ta đặt bốn tam giác nhỏ là ∆OAB, ∆OBC, ∆OCD và ∆ODE và bốn tam giác lớn là ∆OA’B’, ∆OB’C’, ∆OC’D’ và ∆OD’E’ (hình vẽ).

Yêu cầu bài toán đưa về tìm phép vị tự biến ∆OAB, ∆OBC, ∆OCD và ∆ODE lần lượt thành ∆OA’B’, ∆OB’C’, ∆OC’D’ và ∆OD’E’.

Tức là ta đi tìm phép vị tự biến các điểm O, A, B, C, D, E lần lượt thành O, A’, B’, C’, D’, E’.

Ta thấy O là giao điểm của các đường thẳng AA’, BB’, CC’, DD’, EE’.

Ta chứng minh các điểm O, A’, B’, C’, D’, E’ lần lượt là ảnh của các điểm O, A, B, C, D, E qua V_{(O, k)}.

Thật vậy, ta có V_{(O, k)}(A) = A’.

Suy ra $\vec{{OA}^{'}} = k \vec{OA}$ và OA’ = |k|.OA.

Vì A, A’ nằm cùng phía đối với O nên k > 0.

Do đó $k = \frac{{OA}^{'}}{OA}$ .

Mà $k = \frac{{OA}^{'}}{OA} = \frac{{OB}^{'}}{OB}$ nên $\vec{{OB}^{'}} = k \vec{OB}$ , do đó V_{(O, k)}(B) = B’.

Tương tự như trên ta chứng minh được V_{(O, k)}(C) = C’, V_{(O, k)}(D) = D’, V_{(O, k)}(E) = E’.

Vậy $V_{(O, \frac{{OA}^{'}}{OA})}$ là phép vị tự cần tìm.

Lời giải Chuyên đề Toán 11 Bài 6: Phép vị tự hay, chi tiết khác: