Thực hành 2 trang 33 Chuyên đề Toán 11 Chân trời sáng tạo
Giải Chuyên đề Toán 11 Bài 6: Phép vị tự - Chân trời sáng tạo
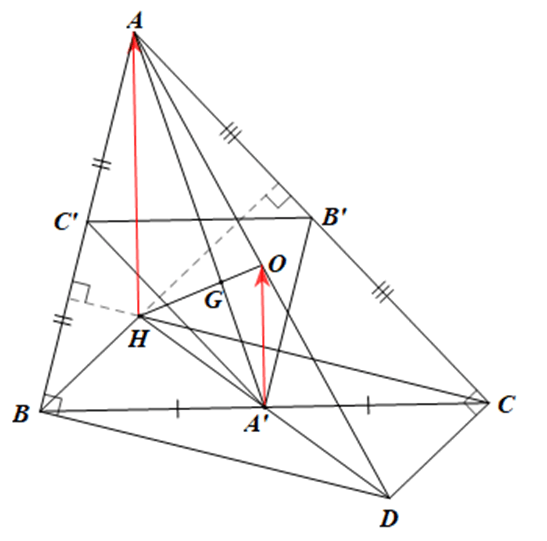
Thực hành 2 trang 33 Chuyên đề Toán 11: Cho tam giác ABC có G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, CA, AB.
a) Tìm phép vị tự biến tam giác ABC thành tam giác A’B’C’.
b) Chứng minh ba điểm H, G, O thẳng hàng.
Lời giải:
a) Để tìm phép vị tự biến ∆ABC thành ∆A’B’C’, ta tìm phép vị tự biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
∆ABC có A’ là trung điểm BC và G là trọng tâm.
Theo tính chất trọng tâm của tam giác, ta có hay .
Suy ra A’ là ảnh của A qua .
Chứng minh tương tự, ta được và .
Vậy biến ∆ABC thành ∆A’B’C’.
b) Gọi AD là đường kính của đường tròn tâm O ngoại tiếp ∆ABC.
Suy ra và O là trung điểm của AD.
Do đó AB ⊥ BD.
Mà CH ⊥ AB (do H là trực tâm của ∆ABC).
Vì vậy BD // CH.
Chứng minh tương tự, ta được BH // CD.
Suy ra tứ giác BHCD là hình bình hành.
Mà A’ là trung điểm BC (giả thiết).
Do đó A’ cũng là trung điểm của DH.
∆ADH có A’O là đường trung bình của tam giác nên và A’O // HA.
Suy ra .
Ta có
.
Khi đó và cùng phương nên ba điểm G, H, O thẳng hàng.
Vậy ba điểm G, H, O thẳng hàng.
Lời giải Chuyên đề Toán 11 Bài 6: Phép vị tự hay, chi tiết khác: