Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các đáy đều bằng a

Bài 4 : Hai mặt phẳng vuông góc

Bài 10 trang 114 Toán 11: Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.

a) Tính độ dài đoạn thẳng SO

b) Gọi M là trung điểm của đoạn SC. Chứng minh rằng hai mặt phẳng (MBD) và ( SAC) vuông góc với nhau.

c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).

Trả lời

a) Ta có: SO ⊥ (ABCD) ⇒ SO ⊥ AC

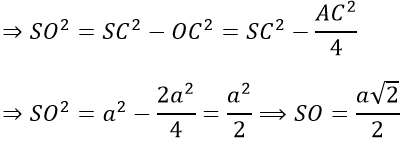
b) Ta có:ABCD là hình vuông ⇒ BD ⊥ AC     (1)

S.ABCD là hình chóp tứ giác đều nên BD ⊥ SO     (2)

(1) và (2) ⇒ BD ⊥ (SAC) ⇒(MBD) ⊥ (SAC)

c) Theo câu a:

Ta có:

Suy ra ∠MOC là góc giữa hai mặt phẳng (MBD) và (ABCD)

Do SOC là tam giác vuông cân ⟹ ∠MOC = 1/2 ∠SOC = 45°