Cho hai mặt phẳng (α), (β) cắt nhau và môt điểm M không thuộc (α) và (β)

Bài 4 : Hai mặt phẳng vuông góc

Bài 4 trang 114 Toán 11: Cho hai mặt phẳng (α), (β) cắt nhau và môt điểm M không thuộc (α) và (β). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với (α) và (β). Nếu (α) // (β) thì kết quả sẽ như thế nào?

Trả lời

Từ M kẻ MH ⊥ (α) và MK ⊥ (β). Gọi ∆ là giao tuyến của (α) và (β).

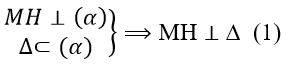
Tương tự ta có: MK ⊥ Δ (2)

Từ (1) và (2) suy ra: Δ ⊥ (MHK)

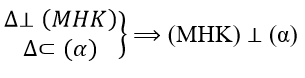
Chứng minh tương tự ta cũng có: (MHK) ⊥ (β)

Vậy mặt phẳng (P) là mặt phẳng (MHK) đi qua M và vuông góc với (α) và (β). Mặt phẳng MHK đi qua M vuông góc với Δ.

Vì qua một điểm chỉ có duy nhất môt mặt phẳng vuông góc với một đường thẳng nên (P) là duy nhất.

Nếu (α) // (β) có vô số mặt phẳng vuông góc với (α) và (β).