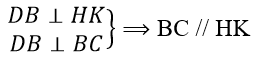Trong mặt phẳng (α) cho tam giác ABC vuông ở B. một đoạn thẳng AD vuông góc

Bài 4 : Hai mặt phẳng vuông góc

Bài 3 trang 113 Toán 11: Trong mặt phẳng (α) cho tam giác ABC vuông ở B. một đoạn thẳng AD vuông góc với (α) tại A. Chứng minh rằng:

a) ∠ABD là góc giữa hai mặt phẳng (ABC) và (DBC)

b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BCD)

c) HK // BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông góc với DB

Trả lời

a) Ta có: DA ⊥ (ABC)

BC ⊥ AB và BC ⊥ DA

⇒ BC ⊥ (ABD) ⇒ BC ⊥ BD

Từ đó ∠ABD là góc giữa hai mặt phẳng (α) và (DBC)

b) Theo câu a thì BC ⊥ (ABD) ⇒ (ABD) ⊥ (BDC)

c) Ta có: (P) ⊥ BD ⇒ DB ⊥ HK

Trong mặt phẳng (ADC) ta có: