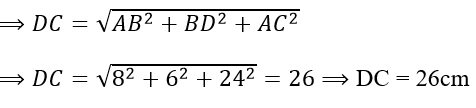Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Người ta lấy trên giáp tuyến

Bài 4 : Hai mặt phẳng vuông góc

Bài 2 trang 113 Toán 11: Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Người ta lấy trên giáp tuyến ∆ của hai mặt phẳng đó hai điểm A và B sao cho AB = 8cm. gọi C là một điểm trê (α) và D là một điểm trên (β) sao cho AC và BD cùng vuông góc với giao tuyến Δ và AC = 6cm, BD = 24cm. tính độ dài đoạn CD.

Trả lời

Trong ∆BAD vuông tại B: AD² = AB² + BD²

Mặt khác: AC ⊥ (β) (định lý)

⇒ AC ⊥ AD ⇒ AD² + AC² = DC²

Từ đó DC² = AB² + BD² + AC²