Cho hình chóp S.ABCD có đáy là một hình thoi tâm I cạnh a và có góc A bằng

Bài 4 : Hai mặt phẳng vuông góc

Bài 11 trang 114 Toán 11: Cho hình chóp S.ABCD có đáy là một hình thoi tâm I cạnh a và có góc A bằng 60°, cạnh SB=(a√6)/2 và SC vuông góc với mặt phẳng (ABCD)

a) Chứng minh rằng mặt phẳng (SBD) vuông góc với mặt phẳng (SAC)

b) Trong tam giác SCA kẻ KI vuông góc với SH tại K. hãy tính độ dài IK

c) Chứng minh ∠BKD = 90º và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD)

Trả lời

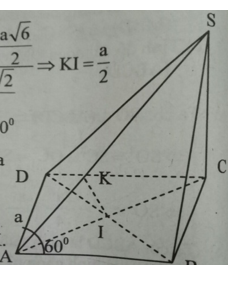
a) Ta có:ABCD là hình thoi ⇒ BD ⊥ AC

SC ⊥ (ABCD) ⇒ BD ⊥ SC. Vậy BD ⊥ (SAC) ⇒ (SBD) ⊥ (SAC) (đpcm)

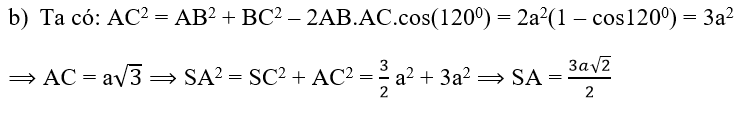
Mặt khác : Hai tam giác AKI và ACS đồng dạng (hai tam giác vuông góc nhọn)

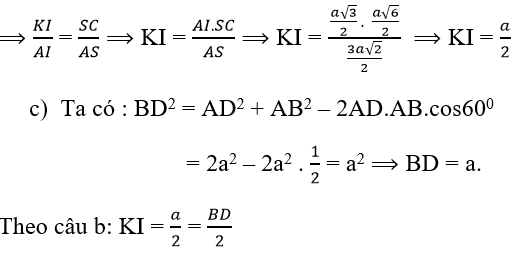
và I là trung điểm BD ⇒ ∆BKD vuông tại K.

Ta có:

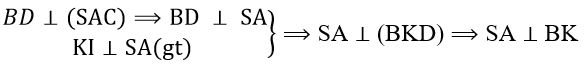
Và vì BK ⊥ DK (chứng minh trên) ⇒ BK ⊥ (SAD) ⇒ (SAD) ⊥ (SAB)