Cho tứ diện S.ABCD có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt

Bài 5 : Khoảng cách

Bài 2 trang 119 Toán 11: Cho tứ diện S.ABCD có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là trực tâm của các tam giác ABC và SBC

a) Chứng minh rằng ba đường thẳng AH, SK, BC đồng quy.

b) Chứng minh rằng SC vuông góc với mặt phẳng (BHK) và HK vuông góc với mặt phẳng (SBC)

c) Xác định đường vuông góc chung của BC và SA.

Trả lời

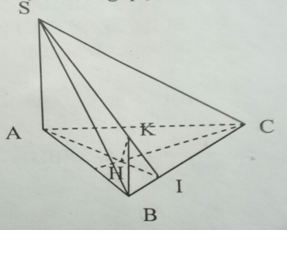
a) Gọi I = AH ∩ BC, ta có:

SA ⊥ (ABC) ⇒ SA ⊥ BC      (1)

AI là đường cao ⇒ BC ⊥ AI      (2)

Từ (1) và (2) ⇒ BC ⊥ (SAI) ⇒ BC ⊥ SI

Ta cũng có BC ⊥ (ASK) ⇒ BC ⊥ SK

Vậy trên mp(SBC) có : SK ⊥ BC ; SI ⊥ C ⇒ I ∈ SK

Vậy AH, BC, SK đồng quy.

b) Ta có : H là trực tâm của ∆ABC ⇒ BH ⊥ AC

SA ⊥ (ABC) ⇒ BH ⊥ SA. Vậy BH ⊥ (SAC) ⇒ BH ⊥ SC   (3)

K là trực tâm của ∆SBC ⇒ BK ⊥ SC    (4)

(3)và (4) ⇒ SC ⊥ (BHK)

c) Rõ ràng: SA ⊥ AI và AI ⊥ BC

Vậy AI là đường thẳng vuông góc chung của BC và SA.