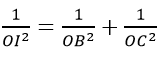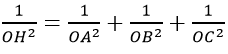Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. H là chân đường

Bài 3 : Đường thẳng vuông góc với mặt phẳng

Bài 4 trang 105 Toán 11: Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng:

a) H là trực tâm của tam giác ABC

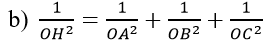
Trả lời

a) OH ⊥ (ABC) ⇒ OH ⊥ AB (1)

OH ⊥ BC (2)

Mặt khác: OA ⊥ OC

OA ⊥ OB

⇒ OA ⊥ ( OBC) (3)

Từ (1) và (3) suy ra BC ⊥ (OAH) ⇒ BC ⊥ AH (4)

Tương tự OC ⊥ OA

OC ⊥ OB

⇒ OC ⊥ ( OAB) (5)

Từ (1) và (5) suy ra AB ⊥ (OCH) ⇒ AB ⊥ CH (6)

Từ (4) và (6) suy ra H là trực tâm của tam giác ABC.

b) Gọi I là chân của đường cao AH trong tam giác ABC

Trong tam giác vuông AOI tại O (OA ⊥ (OBC)), ta có:

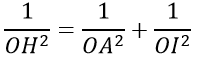
Trong tam giác vuông BOC, ta có:

Vậy