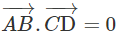Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC

Bài 4: Hai mặt phẳng vuông góc

Bài 3.24 trang 150 Sách bài tập Hình học 11: Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.

Lời giải:

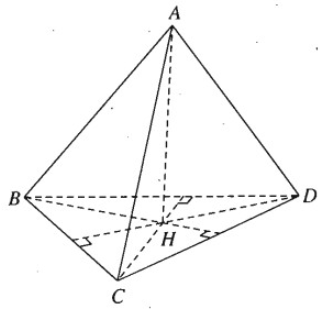
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH

Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC

Vì AH ⊥ BC nên ta suy ra BC ⊥ AD

Cách khác: Trước hết ta hãy chứng minh hệ thức:

với bốn điểm A, B, C, D bất kì.

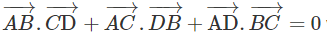
Thực vậy , ta có:

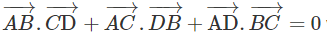
Do đó nếu AB ⊥ CD nghĩa là

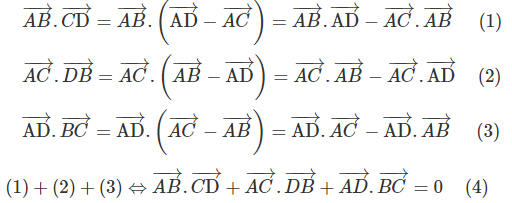
Từ hệ thức (4) ta suy ra , do đó AD ⊥ BC.