Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian

Đề toán tổng hợp chương 2

Bài 2.50 trang 84 Sách bài tập Hình học 11: Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:

MA² + MB² + MC² + MD² đạt giá trị cực tiểu.

Lời giải:

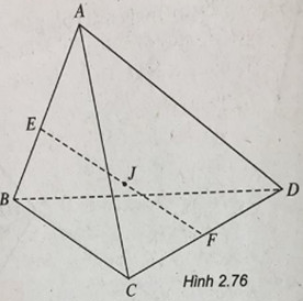
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:

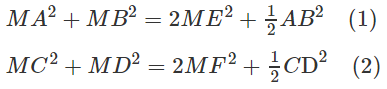
Cộng (1) và (2) ta có:

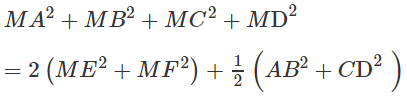
Gọi J là trung điểm của EF, ta có:

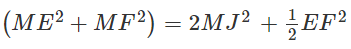
Khi đó:

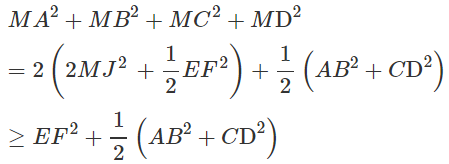
Vậy MA² + MB² + MC² + MD² đạt giá trị nhỏ nhất khi M ≡ J.