Trong mặt phẳng Oxy cho điểm A(2;5). Phép tịnh tiến theo vectơ
Câu hỏi trắc nghiệm chương 1
Bài tập trắc nghiệm trang 39, 40, 41, 42 Sách bài tập Hình học 11:
Bài 1.49: Trong mặt phẳng Oxy cho điểm A(2;5). Phép tịnh tiến theo vectơ v→(1;2) biến A thành điểm có tọa độ
A. (3;1) B. (1;6)
C. (3;7) D. (4;7)
Lời giải:
Dùng công thức:
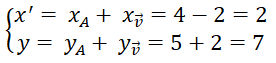
Chọn đáp án: C
Bài 1.50: Trong mặt phẳng tọa độ Oxy cho điểm A(4;5). Qua phép tịnh tiến theo vectơ v→(2;1), A là ảnh của điểm có tọa độ
A. (3;1) B. (1;6)
C. (4;7) D. (2;4)
Lời giải:
Dùng công thức:
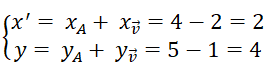
Chọn đáp án: D
Bài 1.51: Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
Lời giải:
Mọi phép tịnh tiến theo vectơ có giá song song hoặc trùng với đường thẳng đều biến đường thẳng thành chính nó. Vậy có vô số phép tịnh tiến.
Chọn đáp án: D
Bài 1.52: Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
Lời giải:
Có một phép tịnh tiến duy nhất theo vectơ 0→.
Chọn đáp án: B
Bài 1.53: Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có bốn D. Vô số
Lời giải:
Có một phép tịnh tiến duy nhất theo vectơ 0→.
Chọn đáp án: B
Bài 1.54: Trong mặt phẳng tọa độ Oxy cho điểm M (2;3), ảnh của M qua phép đối xứng trục Ox có tọa độ
A. (3;2) B. (2;-3)
C. (3;-2) D. (-2;3)
Lời giải:
Phép đối xứng qua trục Ox biến điểm (x;y) thành (x; -y).
Chọn đáp án: B
Bài 1.55: Trong mặt phẳng tọa độ Oxy cho điểm M (2;3), qua phép đối xứng trục Oy thì M là ảnh của điểm có tọa độ
A. (3;2) B. (2;-3)
C. (3;-2) D. (-2;3)
Lời giải:
M(x;y) là ảnh của điểm (-x;y) qua phép đối xứng trục Oy.
Chọn đáp án: D
Bài 1.56: Trong mặt phẳng tọa độ Oxy cho điểm M (2;3), ảnh của M qua phép đối xứng trục là đường thẳng x - y = 0 có tọa độ
A. (3;2) B. (2;-3)
C. (3;-2) D. (-2;3)
Lời giải:
Ảnh của điểm M(x;y) qua phép đối xứng qua đường thẳng x – y = 0 là điểm (y;x).
Chọn đáp án: A
Bài 1.57: Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
Lời giải:
Hình gồm hai đường tròn có tâm và bán kính khác nhau chỉ có một trục đối xứng duy nhất là đường thẳng nối hai tâm đường tròn.
Chọn đáp án: B
Bài 1.58: Khẳng định nào sau đây đúng?
A. Đường tròn là hình có vô số trục đối xứng.
B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn.
C. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm.
D. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vuông góc.
Lời giải:
Đường tròn có trục đối xứng là một đường thẳng bất kì đi qua tâm.
Chọn đáp án: A
Bài 1.59: Trong mặt phẳng Oxy, cho hai điểm I(1;2) và M(3;-1). Ảnh của M qua phép đối xứng tâm I có tọa độ
A. (2;1) B. (-1;5)
C. (-1;3) D. (5;-4)
Lời giải:
Ảnh của M(x;y) qua phép đối xứng tâm I(xo; yo) là (2xo – x; 2yo – y).
Chọn đáp án: B
Bài 1.60: Trong mặt phẳng Oxy, cho đường thẳng Δ có phương trình x = 2. Ảnh của Δ qua phép đối xứng tâm O là đường thẳng
A. x = -2 B. y = 2
C. x = 2 D. y = -2
Lời giải:
Ảnh của Δ: x = a qua phép đối xứng tâm O là đường thẳng x = -a.
Chọn đáp án: A
Bài 1.61: Khẳng định nào sau đây đúng?
A. Phép đối xứng tâm không có điểm nào biến thành chính nó.
B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.
C. Phép đối xứng tâm có hai điểm biến thành chính nó.
D. Phép đối xứng tâm có vô số điểm biến thành chính nó.
Lời giải:
Phép đối xứng tâm I chỉ biến một điểm duy nhất I thành chính nó.
Chọn đáp án: B
Bài 1.62: Trong mặt phẳng Oxy, cho đường thẳng Δ có phương trình x - y + 4 = 0. Đường thẳng Δ là ảnh qua một phép đối xứng tâm của đường thẳng
A. 2x + y - 4 = 0 B. x + y - 1 = 0
C. 2x - 2y + 1 = 0 D. 2x + 2y - 3 = 0
Lời giải:
Đường thẳng có thể biến thành Δ qua một phép đối xứng tâm phải cùng phương với Δ.
Chọn đáp án: C
Bài 1.63: Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
Lời giải:
Hình gồm hai đường tròn phân biệt có cùng bán kính có một tâm đối xứng duy nhất là trung điểm đoạn nối hai tâm.
Chọn đáp án: B
Bài 1.64: Trong mặt phẳng Oxy cho điểm M(1;1). Ảnh của M qua phép quay tâm O, góc 45ο có tọa độ
A. (-1;1) B. (1;0)
C. (√2;0) D. (0; √2)
Lời giải:
Ảnh của M(1;1) qua phép quay tâm O, góc 45o nằm trên tia Oy và cách một đoạn bằng OM = √2. Đó là điểm (0; √2).
Chọn đáp án: D
Bài 1.65: Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π, biến tam giác trên thành chính nó?
A. Chỉ có một B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
Lời giải:
Có ba phép quay tâm O góc α, 0 ≥ α ≥ 2π, biến tam giác trên thành chính nó với α lần lượt bằng: 0; π/2; 3π/2.
Chọn đáp án: D
Bài 1.66: Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π, biến hình vuông trên thành chính nó?
A. Chỉ có một B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
Lời giải:
Có bốn phép quay tâm O góc α, 0 ≥ α ≥ 2π, biến hình vuông trên thành chính nó với α lần lượt bằng: 0; π/2; π; 3π/2.
Chọn đáp án: B
Bài 1.67: Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π, biến hình chữ nhật trên thành chính nó?
A. Không có B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
Lời giải:
Có bốn phép quay tâm O góc α, 0 ≥ α ≥ 2π, biến hình chữ nhật trên thành chính nó với α lần lượt bằng: 0; π.
Chọn đáp án: B
Bài 1.68: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc α ≠ 2kπ, k là một số nguyên?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
Lời giải:
Chỉ có điểm O biến thành chính nó qua phép quay tâm O góc α ≠ 2kπ, k là một số nguyên.
Chọn đáp án: B
Bài 1.69: Trong mặt phẳng Oxy cho điểm M(2;1). Điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ v(2;3) được biến thành điểm có tọa độ
A. (1;3) B. (2;0)
C. (0;2) D. (4;4)
Lời giải:
Sau khi thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ v ⃗(2;3) điểm M(2;1) biến thành điểm có tọa độ
x = -x_M + 2 = -2 + 2 = 0 và y = -y_M + 3 = -1 + 3 = 2.
Chọn đáp án: C
Bài 1.70: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 1)2 + (y + 2)2 = 4. Đường tròn (C) qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ v(2;3) được biến thành đường tròn có phương trình
A. x2 + y2 = 4
B. (x - 2)2 + (y - 6)2 = 4
C. (x - 2)2 + (y - 3)2 = 4
D. (x - 1)2 + (y - 1)2 = 4
Lời giải:
Sau khi thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ v ⃗(2;3) đường tròn (C) biến thành đường tròn (C’) có cùng bán kính và có cùng tâm I’
ẢNHPhương trình của (C’) là (x-1)2 + (y-1)2 = 4.
Chọn đáp án: D
Bài 1.71: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Đường tròn d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ v(2;3) được biến thành đường thẳng có phương trình
A. 3x + 3y - 2 = 0 B. x - y + 2 = 0
C. x + y + 2 = 0 D. x + y - 3 = 0
Lời giải:
D
Chọn đáp án: Lấy điểm M(0;2) trên d. Sau khi thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ v ⃗(3;2) ta được điểm M’(3;0). Đường thẳng d biến thành đường thẳng đi qua M’ và song song với d nên có phương trình x + y – 3 = 0.
Bài 1.72: Khẳng định nào sau đây đúng?
A. Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến.
B. Thực hiện liên tiếp hai phép đối xứng trục sẽ được một phép đối xứng trục.
C. Thực hiện liên tiếp phép đối xứng qua tâm và phép đối xứng trục sẽ được một phép đối xứng qua tâm.
D. Thực hiện liên tiếp phép quay và phép tịnh tiến sẽ được một phép tịnh tiến
Lời giải:
Thực hiện liên tiếp hai phép tịnh tiến theo hai vectơ sẽ được một phép tịnh tiến theo vectơ tổng.
Chọn đáp án: A
Bài 1.73: Khẳng định nào sau đây đúng?
A. Có một phép tịnh tiến theo vectơ khác không biến mọi điểm thành chính nó.
B. Có một phép đối xứng trục biến mọi điểm thành chính nó.
C. Có một phép đối xứng tâm biến mọi điểm thành chính nó.
D. Co một phép quay biến mọi điểm thành chính nó.
Lời giải:
Phép quay với góc quay 2π biến mọi điểm thành chính nó.
Chọn đáp án: D
Bài 1.74: Trong mặt phẳng Oxy cho điểm M(-2;4). Phép vị tự tâm O tỉ số k = -2 biến M thành điểm có tọa độ
A. (-8;4) B. (-4;-8)
C. (4;-8) D. (4;8)
Lời giải:
Phép vị tự tâm O tỉ số k = -2 biến M(x;y) thành điểm M’(-2x; -2y).
Chọn đáp án: C
Bài 1.75: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y - 3 = 0. Phép vị tự tâm O tỉ số k = 2 biến d thành đường thẳng có phương trình
A. 2x + y + 3 = 0 B. 2x + y - 6 = 0
C. 4x - 2y - 3 = 0 D. 4x + 2y - 5 = 0
Lời giải:
Trong phương trình của d, thay x bởi x/2, thay y bởi y/2, ta được phương trình d’ là 2(x/2) + y/2 – 3 = 0 hay 2x + y – 6 = 0.
Chọn đáp án: B
Bài 1.76: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép vị tự tâm O tỉ số k = -2 biến d thành đường thẳng có phương trình
A. 2x + 2y = 0 B. 2x + 2y - 4 = 0
C. x + y + 4 = 0 D. x + y - 4 = 0
Lời giải:
Trong phương trình của d, thay x bởi x/2, thay y bởi y/2, ta được phương trình d’ là: ((-x)/2) + ((-y)/2) – 2 = 0 hay x + y + 4 = 0.
Chọn đáp án: C
Bài 1.77: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 1)2 + (y - 2)2 = 4. Phép vị tự tâm O tỉ số k = -2 biến d thành đường tròn có phương trình
A. (x - 2)2 + (y - 4)2 = 16
B. (x - 4)2 + (y - 2)2 = 4
C. (x - 4)2 + (y - 2)2 = 16
D. (x + 2)2 + (y + 4)2 = 16
Lời giải:
Phép vị tự tâm O tỉ số k = -2 biến (C) tâm I(1;2), bán kính r = 2 thành đường tròn tâm I’(-2; -4), bán kính r’ = 4 và có phương trình(x+2)2 + (y+4)2 = 16.
Chọn đáp án: D
Bài 1.78: Trong mặt phẳng Oxy, cho điểm M(2;4). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 1/2 và phép đối xứng qua trục Oy sẽ biến M thành điểm có tọa độ
A. (1;2) B. (-2;4)
C. (-1;2) D. (1;-2)
Lời giải:
Phép vị tự tâm O tỉ số k = 1/2 biến điểm M(2;4) thành điểm M’(1; 2). Phép đối xứng qua trục Oy sẽ biến M’(1;2) thành điểm M’’(-1;2).
Chọn đáp án: C

