Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau

Bài 3: Đường thẳng vuông góc với mặt phẳng

Bài 14 (trang 102 sgk Hình học 11 nâng cao): Cho điểm S có hình chiếu trên mp(P) là H . Với điểm M bất kì trên (P) (M không trùng H ), ta gọi đoạn thẳng SM là đường xiên , đoạn thẳng HM là hình chiếu của đường xiên đó. Chứng minh rằng :

a) Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau

b) Với đường xiên cho trước , đường xiên nào dài hơn thì có hình chiếu dài hơn và ngược lại , đường xiên nào có hình chiếu ngắn hơn thì ngắn hơn

Lời giải:

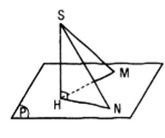
a) Giả sử HM, HN lần lượt là hình chiếu của SM , SN.

- Nếu SM = SN thì ΔSHM = ΔSHN ( cạnh huyền- cạnh góc vuông) nên HM = HN

Ngược lại nếu HM = HN thì

ΔSHM = ΔSHN ( c.g.c) nên SM = SN

Vậy SM = SN ⇔ HM = HN

b) Áp dụng định lí pytago ta có :

SM² = SH² + HM² và SN² = SH² + HN²

Suy ra: SM² - HM² = SN² - HN² (= SH² )

Và SM² - SN² = HM² - HN² . Từ đó suy ra SM > SN ⇔ HM > HN(đpcm)