Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b

Bài 3: Đường thẳng vuông góc với mặt phẳng

Bài 19 (trang 103 sgk Hình học 11 nâng cao): Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC

a) Chứng minh rằng SG ⊥ (ABC) . Tính SG

b) Xét mp(P) đi qua A và vuông góc với đường thẳng SC . Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại C₁ nằm giữa S và C . Khi đó hãy tính diện tích thiết diện của hình chóp S.ABC khi cắt bới mp(P)

Lời giải:

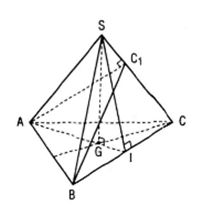
a)Vì SA = SB = SC nên S nằm trên trục của đường thẳng tròn ngoại tiếp tam giác ABC.

Mà tam giác ABC đều có G là tâm đường tròn ngoại tiếp ΔABC

=> G đồng thời là tâm đường tròn ngoại tiếp tam giác ABC: GA = GB = GC

Do đó, G nằm trên trục đường tròn ngoại tiếp tam giác ABC.

=> SG ⊥ (ABC). Gọi I là trung điểm của BC.

Tam giác ABC đều có AI là đường trung tuyến nên đồng thời là đường cao:AI ⊥ BC

Tam giác SBC có SB = SC nên là tam giác cân tại S có SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI