Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC

Bài 3: Đường thẳng vuông góc với mặt phẳng

Bài 18 (trang 103 sgk Hình học 11 nâng cao): Cho hình chóp S.ABC có SA ⊥ mp(ABC), các tam giác ABC và SBC không vuông. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng:

a) AH, SK, BC đồng quy

b) SC ⊥ mp(BHK);

c) HK ⊥ mp(SBC)

Lời giải:

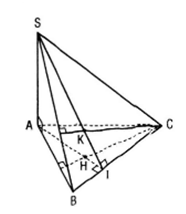
a) Gọi I là giao điểm của hai đường thẳng AH và BC

Ta có BC ⊥ AH (do H là trực tâm ΔABC)

BC ⊥ SA (do SA ⊥ mp(ABC))

⇒ BC ⊥ (SAI) mà SI ⊂ (SAI) nên : BC ⊥ SI (1)

K là trực tâm ΔSBC nên BC ⊥ SK (2)

Từ (1) và (2) suy ra: SI≡SK hay ba điểm S, K, I thẳng hàng.

=> Đường thẳng SK đi qua I

Vậy AH, SK, BC đồng quy tại I

b) Ta có BH ⊥ AC ( vì H là trực tâm tam giác ABC)

và BH ⊥ SA ( vì SA ⊥ mp(ABC)).

Suy ra: BH ⊥ mp(SAC) suy ra BH ⊥ SC

Mặt khác SC ⊥ BK (vì K là trực tâm tam giác SBC)

nên SC ⊥ mặt phẳng(BHK)

c) Ta có SC ⊥ HK (do SC ⊥ mặt phẳng(BHK))

Mà HK ⊥ BC (do BC ⊥ mặt phẳng(SAI))

Vậy HK ⊥ (SBC).