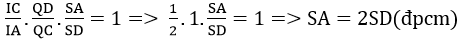Cho tứ diện ABCD . Các điểm P, Q lần lượt là trung điểm

Bài 2: Hai đường thẳng song song

Bài 21 (trang 55 sgk Hình học 11 nâng cao): Cho tứ diện ABCD . Các điểm P, Q lần lượt là trung điểm của AB và CD; Điểm R nằm trên cạnh BC sao cho BR = 2RC . Gọi S là giao điểm của mp(PQR) và cạnh AD , chứng minh rằng AS = 2SD

Lời giải:

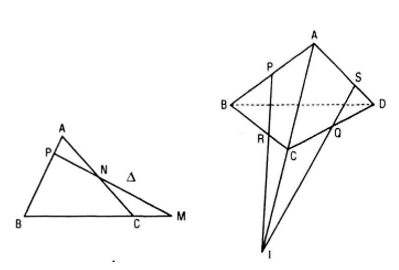
Định lí Menelaus

Giải sử đường thằng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :

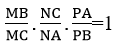
ÁP dụng định lí để giải bài toán

Gọi {I}= PR ∩ AC

Trong mp(ACD) gọi {S} = QI ∩ AD thì

{S} = AD ∩ (PQR)

Áp dụng định lí Menelaus trong ΔABC với cắt tiếp tuyến PRI ta có :

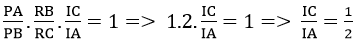
⇒ C là trung điểm của AI

Áp dụng định lí Menelaus trong ΔACD với cát tuyến IQS ta có :