Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC, biết

Ôn tập chương 2

Haylamdo biên soạn và sưu tầm lời giải Bài 2 trang 63 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 2 (trang 63 sgk Hình Học 12 nâng cao): Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC, biết

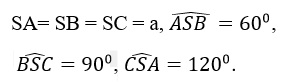
Lời giải:

+ Do tam giác ASB cân tại S và 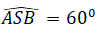nên đây là tam giác đều ⇒ AB= a

+ Tam giác BSC vuông tại S nên BC = a √2

+ Áp dụng định lí cosin trong tam giác ASC ta có:

AC² = SA² + SC² – 2SA. SC. cosA = 3a² nên AC = a √3

Vậy ∆ABC vuông tại B.

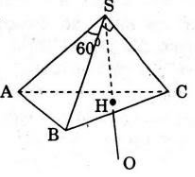
* Gọi SH là đường cao của hình chóp thì do SA = SB = SC nên HA = HB = HC.

Mà tam giác ABC là vuông tại B do đó H là trung điểm của AC.

Gọi O là điểm đối xứng với điểm S qua điểm H.

Ta có:

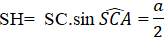
Suy ra; OS= a.

Khi đó OS = OA = OC = OB = a. Suy ra mặt cầu ngoại tiếp hình chóp có tâm O và bán kính R = a.