Cho tứ diện đều ABCD có dạng bằng a. tập hợp các điểm M trong không gian sao cho MA^2+MB^2+MC^2+MD^2=2a^2

Ôn tập chương 2

Haylamdo biên soạn và sưu tầm lời giải Bài 5 trang 64 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 5 (trang 64 sgk Hình Học 12 nâng cao): Cho tứ diện đều ABCD có dạng bằng a. tập hợp các điểm M trong không gian sao cho MA²+MB²+MC²+MD²=2a² là

a) Mặt cầu có tâm là trọng tâm của tam giác ABC và bán kính bằng a√2/2;

b) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng a√2/4

c) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng a√2/2

d) Đường tròn với tâm là trọng tâm tam giác ABC và bán kính bằng a√2/4

Lời giải:

Gọi G là trọng tâm của khối tứ diện ABCD

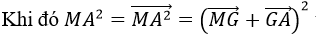
tương tự MB²,MC²,MD²

=> MA²+MB²+MC²+MD²=4MG²+GA²+GB²+GC²+MD²=4MG²+3a²/2 =2a²

=> MG²=a²/8 => M thuộc mặt cầu tâm G, bán kính R = MG = a√2/4. Chọn B