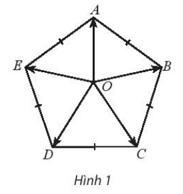
Cho hình ngũ giác đều ABCDE tâm O Chứng minh rằng vecto OA + vecto OB + vecto OC + vecto OD + vecto OE = vecto 0 SBT Toán 10 Tập 1

Haylamdo biên soạn và sưu tầm lời giải Bài 5 trang 103 SBT Toán 10 Tập 1 trong Bài tập cuối chương 5. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải sách bài tập Toán 10 Bài tập cuối chương 5

Bài 5 trang 103 SBT Toán 10 Tập 1: Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: $\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}+\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}=\overrightarrow{0}$.

Lời giải:

Đặt $\overrightarrow{\text{u}}$ = $\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}+\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}$

Ta có: $\overrightarrow{\text{u}}$ = $\overrightarrow{\text{OA}}+\left(\overrightarrow{\text{OB}}+\overrightarrow{\text{OE}}\right)+\left(\overrightarrow{\text{OC}}+\overrightarrow{\text{OD}}\right)$

Do OA nằm trên đường phân giác của $\widehat{\text{BOE}}$ và $\widehat{\text{DOC}}$ của hai tam giác cân BOE và DOC nên ta có các vectơ $\left(\overrightarrow{\text{OB}}+\overrightarrow{\text{OE}}\right)$ và $\left(\overrightarrow{\text{OC}}+\overrightarrow{\text{OD}}\right)$ nằm trên đường thẳng OA, suy ra $\overrightarrow{\text{u}}$ nằm trên đường thẳng OA.

Chứng minh tương tự ta có $\overrightarrow{\text{u}}$ cũng đồng thời nằm trên đường thẳng OB. Như vậy $\overrightarrow{\text{u}}$ = $\overrightarrow{0}$

Vậy $\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}+\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}$ = $\overrightarrow{0}$.