Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình

Sách bài tập Toán 10 Bài tập cuối chương 6

Bài 6.59 trang 26 Sách bài tập Toán lớp 10 Tập 2: Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng

a) y = x² – 3x + 2 và bất phương trình: x² – 3x + 2 ≥ 0;

b) y = x²– x – 6 và bất phương trình: x²– x – 6 < 0.

Lời giải:

Đồ thị hàm số y = x² – 3x + 2 là parabol có bề lõm hướng lên, đỉnh là (1,5; –0,25), đi qua hai điểm (1; 0) và (2; 0). Đồ thị hàm số như hình vẽ:

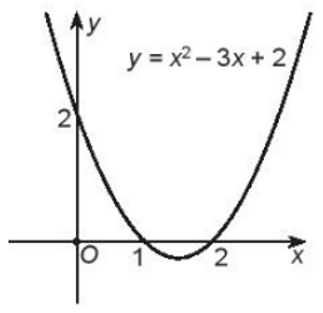
Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình

Việc giải bất phương trình x² – 3x + 2 ≥ 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía trên trục hoành. Từ đồ thị trên ta thấy khi x ≤ 1 và x ≥ 2 thì đồ thị hàm số y = x² – 3x + 2 nằm phía trên trục hoành.

Vậy tập nghiệm của bất phương trình là (–∞; 1]∪[2; +∞).

Đồ thị hàm số y = x²– x – 6 là parabol có bề lõm hướng lên, đỉnh là: (0,5; –6,25), đi qua hai điểm (–2; 0), (3; 0) được vẽ trong hình sau:

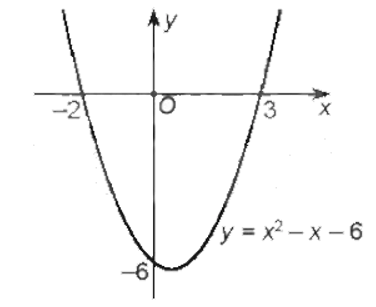
Việc giải bất phương trình y = x²– x – 6 < 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía dưới trục hoành. Từ đồ thị trên ta thấy khi –2 < x < 3 thì đồ thị hàm số y = x²– x – 6 nằm phía dưới trục hoành.

Vậy tập nghiệm của bất phương trình là (–2; 3).

Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Sách bài tập Toán 10 Kết nối tri thức

Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình

Sách bài tập Toán 10 Bài tập cuối chương 6