Ta đã biết rằng hàm cầu liên quan đến giá p của một sản phẩm mới với nhu cầu của người tiêu dùng

Giải sách bài tập Toán 12 Đề minh họa kiểm tra cuối học kì II - Kết nối tri thức

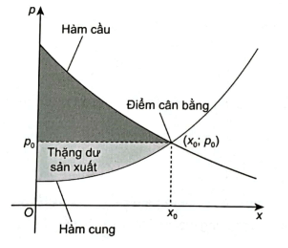
Bài 28 trang 62 SBT Toán 12 Tập 2: Ta đã biết rằng hàm cầu liên quan đến giá p của một sản phẩm mới với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu y = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng. các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong hình vẽ sau:

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: y = −0,01e² + 19 và hàm cung: p = 0,09e^x + 1 trong đó x là số đơn vị sản phẩm. Thặng dư tiêu dung và thặng dư dản xuất cho sản phẩm này lần lượt là (Làm tròn kết quả đến chữ số thập phân thứ hai).

A. 68,01 và 7,57.

B. 68,02 và 7,56.

C. 69,02 và 7,56.

D. 79,02 và 7,66.

Lời giải:

Đáp án đúng là: B

Hoành độ điểm cân bằng là nghiệm của phương trình

−0,01e^x + 19 = 0,09e^x + 1

⇒ 0,1e^x = 18 ⇒ x = ln180.

Suy ra tung độ điểm cân bằng y = 0,09e^ln180 + 1 = 17,2.

Thặng dư sản xuất cho sản phẩm đã cho là:

$\underset{0}{\overset{\ln 180}{\int }}\left|17,2-0,09{\mathrm{e}}^{\mathrm{x}}-1\right|\mathrm{d}\mathrm{x}$≈ 68,02.

Thặng dư tiêu dùng cho sản phẩm đã cho là:

$\underset{0}{\overset{\ln 180}{\int }}\left|-0,01{\mathrm{e}}^{\mathrm{x}}+19-17,2\right|\mathrm{d}\mathrm{x}$ ≈ 7,56.

Lời giải Sách bài tập Toán lớp 12 Đề minh họa kiểm tra cuối học kì II hay khác:

• Bài 1 trang 57 SBT Toán 12 Tập 2: Hàm số F(x) là một nguyên hàm của hàm số f(x) trên khoảng K nếu ....

• Bài 2 trang 57 SBT Toán 12 Tập 2: Nguyên hàm của hàm số f(x) = x⁴ + x² là A. $\frac{1}{5}{\mathrm{x}}^5+\frac{1}{3}{\mathrm{x}}^3+\mathrm{C}$; B. x⁴ + x² + C ....

• Bài 3 trang 57 SBT Toán 12 Tập 2: Biết F(x) = x³ là một nguyên hàm của hàm số f(x) trên ℝ ....

• Bài 4 trang 57 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên ℝ và có $\underset{0}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=9$ ....

• Bài 5 trang 57 SBT Toán 12 Tập 2: Diện tích S của hình phẳng giới hạn bởi các đường y = 2x², y = −1, x = 0 và x = 1 ....

• Bài 6 trang 58 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (P): 3x – z + 2 = 0. Vectơ nào dưới đây ....

• Bài 7 trang 58 SBT Toán 12 Tập 2: Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M(1; 2; −3) ....

• Bài 8 trang 58 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng d: $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}-3}{-5}=\frac{\mathrm{z}+2}{3}$ ....

• Bài 9 trang 58 SBT Toán 12 Tập 2: Trong không gian Oxyz, đường thẳng nào dưới đây đi qua điểm M(6; −2; 1) ....

• Bài 10 trang 59 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt cầu (S): (x + 3)² + (y + 1)² + (z – 1)² = 2 ....

• Bài 11 trang 59 SBT Toán 12 Tập 2: Trong không gian Oxyz, phương trình nào sau đây là phương trình mặt cầu có tâm I(2; −1; −2) ....

• Bài 12 trang 59 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² – 4x + 2y + 3 = 0. Bán kính của mặt cầu (S) là: ....

• Bài 13 trang 59 SBT Toán 12 Tập 2: Cho P(A) = $\frac{2}{7}$; P(B | A) = $\frac{1}{4}$; P(B | $\overline{\mathrm{A}}$) = $\frac{1}{5}$. Giá trị P(B) là ....

• Bài 14 trang 59 SBT Toán 12 Tập 2: Cho hai biến cố A, B sao cho P(A) = 0,4; P(A | B) = 0,7; P(B | A) = 0,3. Tính P($\overline{\mathrm{B}}$) ....

• Bài 15 trang 59 SBT Toán 12 Tập 2: Họ nguyên hàm của hàm số f(x) = 3x² + sinx là ....

• Bài 16 trang 59 SBT Toán 12 Tập 2: Cho $\underset{0}{\overset{\frac{\mathrm{\pi }}{2}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=5$. Tính I = $\underset{0}{\overset{\frac{\mathrm{\pi }}{2}}{\int }}\left[\mathrm{f}\left(\mathrm{x}\right)+2\sin \mathrm{x}\right]\mathrm{d}\mathrm{x}.$ ....

• Bài 17 trang 60 SBT Toán 12 Tập 2: Biết $\underset{1}{\overset{3}{\int }}\frac{\mathrm{x}+2}{\mathrm{x}}\mathrm{d}\mathrm{x}$ = a + blnc, với a, b, c ∈ ℝ, c > 0. Tính tổng S = a + b + c ....

• Bài 18 trang 60 SBT Toán 12 Tập 2: Cho hình phẳng D giới hạn bởi đồ thị hàm số y = $\sqrt{{\mathrm{x}}^2+1}$, trục hoành và hai đường thẳng ....

• Bài 19 trang 60 SBT Toán 12 Tập 2: Cho hai mặt phẳng (α): 3x – 2y + 2z + 7 = 0, (β): 5x – 4y + 3z + 1 = 0 ....

• Bài 20 trang 60 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho ba điểm A(1; −2; 3), B(2; 0; 1), C(3; −2; 0). Phương trình mặt phẳng đi qua A, B, C là ....

• Bài 21 trang 60 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho điểm A(1; 2; −1) và mặt phẳng (P): x + 3y – 2z – 1 = 0 ....

• Bài 22 trang 61 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho hai điểm M(1; 0; 1) và N(3; 2; −1). Đường thẳng MN có phương trình tham số là ....

• Bài 23 trang 61 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho hai điểm A(2; 4; 1), B(−2; 2; −3). Phương trình mặt cầu đường kính AB là ....

• Bài 24 trang 61 SBT Toán 12 Tập 2: Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên ....

• Bài 25 trang 61 SBT Toán 12 Tập 2: Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên một viên bi ....

• Bài 26 trang 61 SBT Toán 12 Tập 2: Một xạ thủ bắn vào bia số 1 và bia số 2. Xác suất để xạ thủ đó bắn trúng bia số 1 ....

• Bài 27 trang 62 SBT Toán 12 Tập 2: Họ nguyên hàm của hàm số y = ${\mathrm{e}}^{\mathrm{x}}\left(2+\frac{{\mathrm{e}}^{-\mathrm{x}}}{{\cos }^2\mathrm{x}}\right)$ là ....

• Bài 29 trang 63 SBT Toán 12 Tập 2: Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó ....

• Bài 30 trang 63 SBT Toán 12 Tập 2: Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz ....

• Bài 31 trang 63 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho các đường thẳng: (d₁): $\frac{\mathrm{x}-3}{1}=\frac{\mathrm{y}+1}{-2}=\frac{\mathrm{z}+1}{1}$ ....

• Bài 32 trang 64 SBT Toán 12 Tập 2: Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là α°N, β°E (0 < α, β < 90) ....

• Bài 33 trang 64 SBT Toán 12 Tập 2: Có hai chuồng thỏ. Chuồng I có 6 con thỏ đen và 10 con thỏ trắng ....

• Bài 34 trang 64 SBT Toán 12 Tập 2: Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là 0,01%. Nếu một người mắc bệnh ....

• Bài 35 trang 64 SBT Toán 12 Tập 2: Có hai đội thi đấu môn bắn súng. Đội I có 6 vận động viên, dội II có 8 vận động viên ....

• Bài 36 trang 65 SBT Toán 12 Tập 2: Hình bên dưới là một cánh cửa gỗ, phần dưới có dạng hình chữ nhật ABCD ....

• Bài 37 trang 65 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (P): x + 2y – 2z + 3 = 0 và đường thẳng d: $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{-1}=\frac{\mathrm{z}}{1}$ ....

• Bài 38 trang 65 SBT Toán 12 Tập 2: Trong một hộp kín có 10 chiếc bút bi xanh và 6 chiếc bút bi đỏ đều có kích thước và khối lượng như nhau ....