Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ

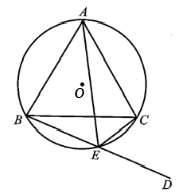
Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.

Giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều

Bài 16 trang 90 SBT Toán 9 Tập 2: Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.

Lời giải:

⦁ Vì ∆ABC đều nên $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60°.$

Do tứ giác ABEC nội tiếp đường tròn nên tổng hai góc đối nhau bằng 180°, suy ra $\widehat{CEB}+\widehat{BAC}=180°$

Mà $\widehat{CEB}+\widehat{CED}=180°$ (hai góc kề bù)

Do đó $\widehat{CED}=\widehat{BAC}=60°\left(=180°-\widehat{BEC}\right).$

Xét đường tròn (O) có $\widehat{AEC}=\widehat{ABC}=60°$ (hai góc nội tiếp cùng chắn cung AC) nên $\widehat{AEC}=\widehat{CED}=60°.$

Do đó, EC là đường phân giác của góc AED.

⦁ Tương tự ta có $\widehat{AEC}=\widehat{ABC}=60°$ và $\widehat{AEB}=\widehat{ACB}=60°.$

Do đó $\widehat{AEB}=\widehat{AEC}=60°$ hay EA là đường phân giác của góc BEC.

Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay khác:

• Bài 12 trang 90 SBT Toán 9 Tập 2: Tìm phát biểu sai trong các phát biểu sau ....

• Bài 13 trang 90 SBT Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo mỗi góc còn lại của tứ giác đó trong mỗi trường hợp sau ....

• Bài 14 trang 90 SBT Toán 9 Tập 2: Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm ....

• Bài 15 trang 90 SBT Toán 9 Tập 2: Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung ....

• Bài 17 trang 90 SBT Toán 9 Tập 2: Cho tam giác ABC cân ở A, H là trung điểm của BC và ....

• Bài 18 trang 91 SBT Toán 9 Tập 2: Cho $\widehat{xAy}=60°$ và điểm B nằm trong góc xAy. Kẻ đường thẳng BN vuông góc ....

• Bài 19 trang 91 SBT Toán 9 Tập 2: Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Đường thẳng qua C ....

• Bài 20 trang 91 SBT Toán 9 Tập 2: Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn ....

• Bài 21 trang 91 SBT Toán 9 Tập 2: Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó ....

• Bài 22* trang 91 SBT Toán 9 Tập 2: Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý ....