Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý
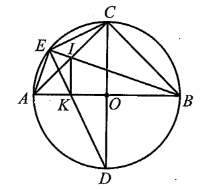
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều
Bài 22* trang 91 SBT Toán 9 Tập 2: Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Lời giải:
Kẻ đường kính CD, khi đó ta có điểm D cố định.
Ta có (góc nội tiếp chắn nửa đường tròn (O) đường kính AB) và (do IK ⊥ AB) nên hai điểm E, K cùng thuộc đường tròn đường kính AI.
Do đó tứ giác EIKA nội tiếp đường tròn đường kính AI.
Suy ra (hai góc nội tiếp cùng chắn cung KI).
Lại có (do ∆ACB vuông cân tại C) do đó hay (1)
Mặt khác, ∆ABC vuông cân tại C có CO là đường trung tuyến nên đồng thời là đường cao, đường phân giác của tam giác.
Do đó
Mà là hai góc nội tiếp cùng chắn cung BD của đường tròn (O) nên (2)
Từ (1) và (2) suy ra E, K, D thẳng hàng.
Vậy khi điểm E di chuyển trên cung nhỏ AC thì EK luôn đi qua điểm D cố định.
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay khác: