Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Đường thẳng qua C vuông góc
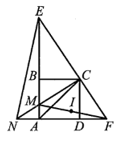
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Đường thẳng qua C vuông góc với CM cắt các tia AB, AD lần lượt tại E và F. Tia CM cắt đường thẳng AD tại N. Chứng minh rằng:
Giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều
Bài 19 trang 91 SBT Toán 9 Tập 2: Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Đường thẳng qua C vuông góc với CM cắt các tia AB, AD lần lượt tại E và F. Tia CM cắt đường thẳng AD tại N. Chứng minh rằng:
a) và
b) CM + CN = EF.
Lời giải:
a) Gọi I là trung điểm của MF.
Xét ∆CMF vuông tại C nên điểm C nằm trên đường tròn đường kính MF.
Do ABCD là hình vuông nên ∆MAF vuông tại A, do đó điểm A nằm trên đường tròn đường kính MF.
Khi đó, bốn điểm A, M, C, F cùng nằm trên đường tròn đường kính MF, do đó tứ giác AMCF nội tiếp đường tròn đường kính MF.
Suy ra (hai góc nội tiếp cùng chắn cung MA) hay
Tương tự, ta chứng minh được tứ giác NACE nội tiếp đường tròn đường kính NE, nên (hai góc nội tiếp cùng chắn cung NA).
b) Do ABCD là hình vuông nên AC là đường phân giác của do đó hay
Ta có tứ giác NACE nội tiếp đường tròn nên (hai góc nội tiếp cùng chắn cung EC).
Mà nên tam giác CEN vuông cân tại C.
Vì thế CN = CE.
Tương tự, tam giác CMF vuông cân tại C suy ra CM = CF.
Do đó CM + CN = CF + CE = EF.
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay khác: