Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn
Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn.
Giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều
Bài 20 trang 91 SBT Toán 9 Tập 2: Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn.
Lời giải:
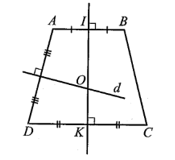
Gọi IK là trục đối xứng của hình thang cân ABCD.
Gọi đường trung trực d của AD. Gọi O là giao điểm của d và IK.
Khi đó, OA = OB = OC = OD suy ra các điểm A, B, C, D đều thuộc đường tròn tâm O, bán kính OA hay hình thang cân ABCD nội tiếp đường tròn.
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay khác: