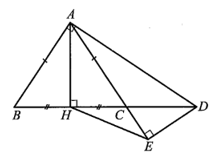
Cho tam giác ABC cân ở A, H là trung điểm của BC và góc BAC nhỏ hơn 90 độ
Cho tam giác ABC cân ở A, H là trung điểm của BC và Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh:
Giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn - Cánh diều
Bài 17 trang 90 SBT Toán 9 Tập 2: Cho tam giác ABC cân ở A, H là trung điểm của BC và Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh:
a) AH = EH;
b)
Lời giải:
a) Do tam giác ABC cân tại A có AH là trung tuyến của tam giác nên đồng thời là đường cao của tam giác và đường phân giác của góc BAC, nên (1)
Do ∆AHD vuông tại H nên H thuộc đường tròn đường kính AD.
Do ∆AED vuông tại E nên E thuộc đường tròn đường kính AD.
Do đó tứ giác AHED nội tiếp đường tròn đường kính AD, suy ra (2) (hai góc nội tiếp cùng chắn cung AH).
Mặt khác (3) (vì cùng phụ với
Từ (1), (2) và (3) suy ra
Do đó, tam giác HAE cân tại H nên AH = EH.
b) Xét ∆AHB và ∆AHC có:
AB = AC (do ∆ABC cân tại A);
HB = HC (do H là trung điểm của BC);
AH là cạnh chung
Do đó ∆AHB = ∆AHC (c.c.c)
Suy ra (hai góc tương ứng).
Mà nên
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp đường tròn hay khác: