Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng y = ax^2
Giải SBT Toán 9 Bài tập cuối chương 7 - Cánh diều
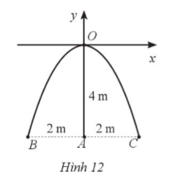
Bài 37* trang 73 SBT Toán 9 Tập 2: Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng y = ax2, gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
Lời giải:
Từ Hình 12, ta thấy C(2;–4).
Đồ thị hàm số y = ax2 đi qua C(2;–4) nên thay x = 2; y = ‒4 vào hàm số ta có:
–4 = a.22 hay 4a = –4, suy ra a = –1.
Do đó, y = –x2.
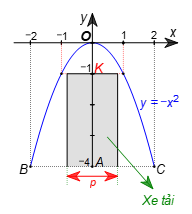
Chiều cao của chiếc xe tải là 3m nên mái xe của chiếc xe tải còn cách vị trí cao nhất của cổng một khoảng là 4 – 3 = 1 (m).
Gọi K(0;–1) nằm trên trục Oy.
Thay y = –1 vào hàm số y = –x2, ta được –1 = –x2, hay x2 = 1 nên x = –1 hoặc x = 1.
Để chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng mà không chạm vào cổng thì p < 1 + 1 hay p < 2.
Dễ thấy, nếu p < 2 thì chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng sẽ không chạm vào cổng.
Vậy p < 2.
Lời giải SBT Toán 9 Bài tập cuối chương 7 hay khác:
Bài 34 trang 72 SBT Toán 9 Tập 2: Hàm số nào dưới đây có đồ thị là đường cong ở Hình 11? ....
Bài 38 trang 73 SBT Toán 9 Tập 2: Giải các phương trình: a) b) 9x2 – 17x + 4 = 0; ....
Bài 39 trang 73 SBT Toán 9 Tập 2: Không tính ∆, giải các phương trình: a) ....