Cho tam giác ABC nội tiếp đường tròn (O), vẽ AX ⊥ BC và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD
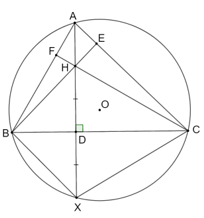
Cho tam giác ABC nội tiếp đường tròn (O), vẽ AX ⊥ BC và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho DH = DX. Cho BH cắt AC tại E và CH cắt AB tại F.
Giải sách bài tập Toán 9 Bài tập ôn tập cuối năm - Kết nối tri thức
Bài 14 trang 73 sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O), vẽ AX ⊥ BC và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho DH = DX. Cho BH cắt AC tại E và CH cắt AB tại F.
a) Chứng minh rằng H là trực tâm của tam giác ABC.
b) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF.
Lời giải:
a) Xét ∆BDH và ∆BDX có:
Chung cạnh BD
DH = DX
Do đó ∆BDH = ∆BDX (c.g.c), suy ra (hai góc tương ứng).
Vì và là hai góc nội tiếp của (O) cùng chắn cung nên
Do đó
Suy ra
Xét tam giác EBC có
Suy ra
Suy ra BE ⊥ AC.
Do đó H là giao điểm hai đường cao AD và BE nên H là trực tâm của tam giác ABC và CF ⊥ AB (đpcm).
b) Tam giác HDB vuông tại D nên tam giác HDB nội tiếp đường tròn đường kính HB.
Tam giác HFB vuông tại F nên tam giác HFB nội tiếp đường tròn đường kính HB.
Do đó tứ giác BDHF nội tiếp đường tròn đường kính HB.
Vì và là hai góc nội tiếp cùng chắn cung của đường tròn đường kính HB nên
Tương tự, ta được tứ giác HECD nội tiếp đường tròn đường kính HC, suy ra
Tam giác ABE vuông tại E nên ta có:
Tương tự với tam giác ACF ta được , suy ra
Từ đó suy ra
Do đó H nằm trên đường phân giác của góc EDF.
Tương tự ta có H nằm trên đường phân giác của góc FED.
Vậy H là tâm đường tròn nội tiếp tam giác DEF. (đpcm)
Lời giải SBT Toán 9 Bài tập ôn tập cuối năm hay khác:
Bài 2 trang 72 sách bài tập Toán 9 Tập 2: Cho hệ phương trình: .Giải hệ phương trình với m = 1 ...
Bài 3 trang 72 sách bài tập Toán 9 Tập 2: Giải bất phương trình –10x + 7 > 3x – 4. ...
Bài 4 trang 72 sách bài tập Toán 9 Tập 2: Cho biểu thức: (x ≥ 0, x ≠ 4). ...