Bài 7 trang 100 Toán 10 Tập 1 Cánh diều

---

Chứng minh:

Giải Toán lớp 10 Bài tập cuối chương 4

Bài 7 trang 100 Toán lớp 10 Tập 1: Chứng minh:

a) Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AE}$ với E là điểm bất kì; 

b) Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MN}$ với M, N là hai điểm bất kì; 

c) Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{NG}$ với M, N là hai điểm bất kì. 

Lời giải:

a) 

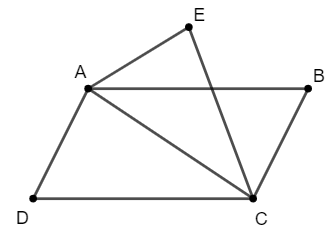
Vì ABCD là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$. 

Với E là điểm bất kì ta có: 

$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AC}+\overrightarrow{CE}=\overrightarrow{AE}$. 

Vậy $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AE}$ với E là điểm bất kì. 

b) 

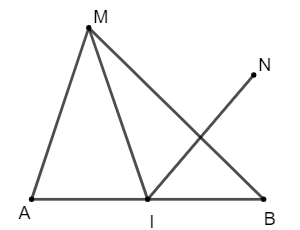
Vì I là trung điểm của AB nên với điểm M bất kì ta có: $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$. 

Do đó, với điểm N bất kì, ta có: 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MI}+2\overrightarrow{IN} \\ =2\left(\overrightarrow{MI}+\overrightarrow{IN}\right)=2\overrightarrow{MN} \end{gathered}$$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MN}$ với M, N là hai điểm bất kì. 

c) 

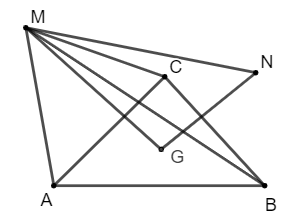
Do G là trọng tâm của tam giác ABC nên với điểm M bất kì ta có: 

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$. 

Khi đó với điểm N bất kì ta có: 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{MG}-3\overrightarrow{MN} \\ =3\left(\overrightarrow{MG}+\left(-\overrightarrow{MN}\right)\right)=3\left(\overrightarrow{MG}+\overrightarrow{NM}\right) \\ =3\left(\overrightarrow{NM}+\overrightarrow{MG}\right)=3\overrightarrow{NG} \end{gathered}$$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{NG}$ với M, N là hai điểm bất kì. 

Lời giải bài tập Toán 10 Bài tập cuối chương 4 trang 99, 100 hay, chi tiết khác:

• Bài 1 trang 99 Toán lớp 10 Tập 1: : Cho tam giác ABC có AB = 3, AC = 4, $\widehat{BAC}=120°$. Tính (làm tròn kết quả đến hàng đơn vị): ....

• Bài 2 trang 99 Toán lớp 10 Tập 1: Không dùng máy tính cầm tay, hãy tính giá trị của các biểu thức sau: ....

• Bài 3 trang 99 Toán lớp 10 Tập 1: Không dùng thước đo góc, làm thế nào để biết số đo góc đó. ....

• Bài 4 trang 99 Toán lớp 10 Tập 1: Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và từ B đến C, người ta làm như sau (Hình 70): ....

• Bài 5 trang 99, 100 Toán lớp 10 Tập 1: Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau). ....

• Bài 6 trang 100 Toán lớp 10 Tập 1: Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN ....

• Bài 8 trang 100 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có AB = 4, AD = 6, $\widehat{BAD}=60°$ (Hình 74) ....

• Bài 9 trang 100 Toán lớp 10 Tập 1: Hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc $\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)=\alpha$ làm cho vật di chuyển theo hướng từ O đến C (Hình 74). ....