Cho góc góc xOy=30 độ. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1
Câu hỏi:
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
A.
B.
C.
D. 2
Trả lời:
Đáp án đúng là: B
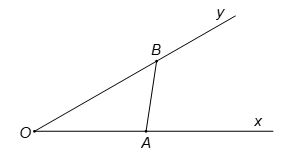
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi: .
Khi đó OB = 2. Tam giác OAB vuông tại .
Xem thêm bài tập Toán 10 Cánh diều có lời giải hay khác:
Câu 1:
Tam giác ABC có . Số đo góc bằng:
Xem lời giải »
Câu 2:
Tam giác ABC có và . Tính độ dài cạnh BC.
Xem lời giải »
Câu 3:
Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và . Tính độ dài cạnh cạnh BC.
Xem lời giải »
Câu 4:
Tam giác ABC có và . Tính độ dài cạnh BC.
Xem lời giải »
Câu 5:
Tam giác ABC có . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức . Khi đó góc bằng bao nhiêu độ?
Xem lời giải »
Câu 6:
Tam giác ABC vuông tại A, có . Gọi m là độ dài đoạn phân giác trong góc . Tính m theo b và c.
Xem lời giải »
Câu 7:
Tam giác ABC có BC = 10 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Xem lời giải »


