Luyện tập 4 trang 96 Toán 10 Tập 1 Cánh diều

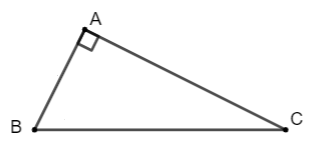
Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC = AB + AC

Giải Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ

Luyện tập 4 trang 96 Toán lớp 10 Tập 1: Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC² = AB² + AC²

Lời giải:

+ Ta chứng minh định lí thuận:

Có tam giác ABC vuông ở A, cần chứng minh BC² = AB² + AC².

Luyện tập 4 trang 96 Toán 10 Tập 1 Cánh diều

Tam giác ABC vuông tại A nên $\hat{B A C} = 90 °$ .

Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$

Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$

= AB² + AC² – 2 . AC . AB . cosA

= AB² + AC² – 2 . AC . AB . cos 90°

= AB² + AC² – 2 . AC . AB . 0

= AB² + AC².

Vậy BC² = AB² + AC².

+ Ta chứng minh định lí đảo:

Cho tam giác ABC có BC² = AB² + AC² thì tam giác ABC vuông tại A.

Luyện tập 4 trang 96 Toán 10 Tập 1 Cánh diều

Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$

Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$ (*)

Mà theo giả thiết ta có: BC² = AB² + AC² nên thay vào (*) ta được:

BC² = BC² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$

Suy ra: 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$ = 0

$\Leftrightarrow \cos (\vec{A C}, \vec{A B}) = 0$ hay $\cos \hat{B A C} = 0$

Do đó: $\hat{B A C} = 90 °$ .

Vậy tam giác ABC vuông tại A.

Lời giải bài tập Toán 10 Bài 6: Tích vô hướng của hai vectơ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 10 Cánh diều

Luyện tập 4 trang 96 Toán 10 Tập 1 Cánh diều

Giải Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: